5. Магнитная энергия тока. Объемная плотность энергии магнитного поля.
1. Энергия магнитного поля.
Рассмотрим
цепь на рис.4. При замкнутом ключе в соленоиде течет ток I, который создаст в нем магнитное поле. При размыкании
через R будет течь некоторое время убывающий ток,
поддерживаемый ЭДС самоиндукции. Работа этого тока за dt равна
![]() При L = const подставим
При L = const подставим ![]() , тогда
, тогда ![]() . Интегрируя от начального I до 0, получим работу в цепи за время исчезновения магнитного поля:
. Интегрируя от начального I до 0, получим работу в цепи за время исчезновения магнитного поля:
![]() ,которая идет на нагрев
всех элементов цепи. Других изменений нет, исчезло только магнитное поле,
которое и является носителем энергии. Т.О.
,которая идет на нагрев
всех элементов цепи. Других изменений нет, исчезло только магнитное поле,
которое и является носителем энергии. Т.О.
![]() . (8)
. (8)
Выразим W через характеристики поля. Тогда с учетом ![]() и H = n I, откуда
и H = n I, откуда
![]() , подучим
, подучим
![]() . (9)
. (9)
Отсюда
плотность энергии магнитного поля равна
![]() . (10)
. (10)
1. Явление электромагнитной индукции. Основной закон электромагнитной индукции. Правило Ленца.
2 В
Согласно Фарадею, индукционный ток можно
вызвать двумя способами: 1 способ - перемещение рамки Р или ее частей с
гальванометром (индикатором индукционного тока) в поле неподвижной катушки К с
током, создающей магнитное поле; 2 способ – рамка Р неподвижна, но изменяется
магнитное поле (либо за счет движения катушки, либо вследствие изменения силы
тока, либо в результате того и другого вместе).

Закон электромагнитной индукции.
![]() . (1)
. (1)
ЭДС индукции равна скорости
изменения магнитного потока, взятой с обратным знаком. Знак «минус» физически
обусловлен правилом Ленца. Геометрически это связано с правилом знаков.
Правило Ленца: Индукционный ток всегда направлен так, чтобы
противодействовать причине, его вызывающей. Проще для понимания – индукционный
ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего
индукционный ток.
Если приближать Р к К, возрастет магнитный
поток через Р, тогда в Р возникнет индукционный ток, направленный так
(например, по часовой стрелке при наблюдении справа), что он создает магнитный
поток, «направленный» влево и уменьшающий исходный поток.
То же произойдет при увеличении силы тока
в К при неподвижных К и Р.
Направление IИНД
изменится при удалении Р или уменьшении силы тока в К.
Правило
Ленца соответствует положению, согласно которому система стремится противодействовать
изменению ее состояния. В этом проявляется электромагнитная
инерция.
2. Явление самоиндукции. Индуктивность контура. Индуктивность длинного прямого соленоида.
3 Явление самоиндукции наблюдается, если в некотором контуре течет
изменяющийся во времени ток. ~ I→ ~B → ~Ф → IИНД.
![]() Если в
окружающем пространстве нет ферромагнетиков, то индукция В и, следовательно,
Если в
окружающем пространстве нет ферромагнетиков, то индукция В и, следовательно, ![]() через контур будут пропорциональны I:
через контур будут пропорциональны I:
![]() , (3)
, (3)
где
L – индуктивность контура. ![]() и I всегда имеют
одинаковые знаки, поэтому L > 0.
и I всегда имеют
одинаковые знаки, поэтому L > 0.
L зависит от формы и размеров контура и магнитных свойств окружающей среды.
L = const при отсутствии поблизости от
контура ферромагнетиков.
![]() .
.
Пример: Индуктивность соленоида.
![]() , в соленоиде при токе
I магнитное поле
, в соленоиде при токе
I магнитное поле ![]() . Тогда
. Тогда ![]() и
и
![]() , откуда
, откуда ![]() . (4)
. (4)
ЭДС
самоиндукции можно переписать в виде:![]() , (5)
, (5)
если
L = const.
Примеры проявления самоиндукции – токи размыкания
и замыкания цепи.
![]() и
и ![]() . (6)
. (6)
Вводят
понятие постоянной времени цепи – время релаксации: ![]() . (7)
. (7)
3. Экстратоки размыкания и замыкания в электрических цепях.
4 Экстратоки размыкания и замыкания в
электрических цепях.
При всяком изменении силы тока
в проводящем контуре возникает эдс самоиндукции, в рез-те чего в контуре
появляются дополнительные токи, наз экстратоками самоиндукции.
Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены противоположно
току, создаваемому источником. Наличие индуктивности в цепи приводит к
замедлению исчезновения или установления тока в цепи.
Процесс включения тока в цепи
(источник тока с эдс, резистор R, катушка L). Под действием внешней эдс в цепи течет постоянный
ток ![]() . В момент t=0 отключим источник тока, ток в катушке начнет
уменьшаться, что приведет к возникновению эдс самоиндукции
. В момент t=0 отключим источник тока, ток в катушке начнет
уменьшаться, что приведет к возникновению эдс самоиндукции ![]() , препятствующий уменьшению тока. В каждый момент времени ток
в цепи опред-ся з-ном Ома
, препятствующий уменьшению тока. В каждый момент времени ток
в цепи опред-ся з-ном Ома ![]() , или
, или ![]()
![]()
![]() или
или ![]() , где
, где ![]() - время релаксации- время в теч-ие к-ого сила тока
уменьшается в е раз.
- время релаксации- время в теч-ие к-ого сила тока
уменьшается в е раз.
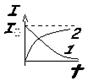
В процессе отключения
источника тока сила тока убывает по экспоненциальному з-ну и опред-ся кривой 1.
чем больше индуктивность цепи и меньше ее сопротивление, тем больше ![]() и, след-но, тем
медленнее уменьшается ток в цепи при ее размыкании
и, след-но, тем
медленнее уменьшается ток в цепи при ее размыкании
При замыкании цепи помимо внешней эдс возникает эдс самоиндукции ![]() , препятствующая возрастанию тока. По з-ну Ома
, препятствующая возрастанию тока. По з-ну Ома ![]() или
или ![]()
![]()
![]()
![]() , где
, где ![]() - установившийся ток (при
- установившийся ток (при ![]()
![]() )
)
В процессе включения источника
тока нарастание силы тока в цепи
опред-ся кривой 2. Сила тока возрастает от начального значения I=0 и асимптотически стремится к установившемуся значению
![]() . Скорость нарастания тока опред-ся
. Скорость нарастания тока опред-ся ![]() . Установление тока происходит тем быстрее, чем меньше
индуктивность цепи и больше ее сопротивление
. Установление тока происходит тем быстрее, чем меньше
индуктивность цепи и больше ее сопротивление
 эдс самоиндукции
эдс самоиндукции ![]() , т.е. при значительном увеличении сопротивления цепи(
, т.е. при значительном увеличении сопротивления цепи(![]() ), обладающей большой индуктивностью, эдс самоиндукции может
во много раз превышать эдс источника тока, включенного в цепь
), обладающей большой индуктивностью, эдс самоиндукции может
во много раз превышать эдс источника тока, включенного в цепь
4. Явление взаимной индукции. Коэффициент взаимной индуктивности контуров.





7. Ток смещения. Система уравнений Максвелла для электромагнитного поля. Относительность электрических и магнитных полей.
5 Ток смещения
Теория электромагнитного поля, начала которой
заложил Фарадей, математически была завершена Максвеллом. При этом важную роль
сыграла его идея или гипотеза, что меняющееся во времени электрическое поле
создает магнитное поле. Это может следовать из следующих рассуждений.
Применим теорему о циркуляции вектора ![]() :
: ![]() (1) к случаю разрядки заряженного плоского
конденсатора через некоторое сопротивление (рис.2). Выберем контур в виде
охватывающей провод кривой. На этот контур могут опираться две поверхности S1 и S2, но через S2 течет ток
а через S1 нет, т.е.
циркуляция вектора
(1) к случаю разрядки заряженного плоского
конденсатора через некоторое сопротивление (рис.2). Выберем контур в виде
охватывающей провод кривой. На этот контур могут опираться две поверхности S1 и S2, но через S2 течет ток
а через S1 нет, т.е.
циркуляция вектора ![]() зависит от выбора поверхности, чего не должно быть и не было
для постоянных токов (стационарных полей).
зависит от выбора поверхности, чего не должно быть и не было
для постоянных токов (стационарных полей).
Чтобы
избавиться от этого противоречия, используем теорему Гаусса для вектора ![]() :
:
![]() , откуда
, откуда ![]() . (2)
. (2)
и
уравнение непрерывности
![]() . (3)
. (3)
Сложим
(2) и (3): ![]() . (4)
. (4)
Получено
Ур.(4), аналогичное уравнению непрерывности для постоянного тока.
![]() - плотность тока
смещения. (5)
- плотность тока
смещения. (5)
Плотность
полного тока ![]() . (6)
. (6)
Теперь ![]() . (7) и
. (7) и
![]() . (8)
. (8)
для общего случая
(нестационарных полей). Вспомним, что ![]() , т.е. плотность тока смещения складывается из «истинного»
тока смещения
, т.е. плотность тока смещения складывается из «истинного»
тока смещения ![]() и тока поляризации
и тока поляризации ![]() (движения связанных зарядов). Принципально новым является то,
что изменение электрического поля возбуждает магнитное поле.
(движения связанных зарядов). Принципально новым является то,
что изменение электрического поля возбуждает магнитное поле.
6. Фарадеевская и максвелловская трактовки явления электромагнитной индукции. Вихревое электрическое поле. Первое уравнение Максвелла.
Система уравнений Максвелла (в неподвижных средах)
Она представляет, по существу,
единую теорию электрических и магнитных явлений.
В интегральной форме:
![]() ,
, ![]() (9)
(9)
![]() ,
, ![]() . (10)
. (10)
Выразим физический смысл
каждого уравнения.
Из выражений для циркуляций ![]() и
и ![]() следует, что электрическое и магнитное поля нельзя
рассматривать как независимые: изменение во времени одного из полей приводит к
появлению другого. Поэтому имеет смысл лишь совокупность этих полей, представляющая
собой единое электромагнитное поле.
следует, что электрическое и магнитное поля нельзя
рассматривать как независимые: изменение во времени одного из полей приводит к
появлению другого. Поэтому имеет смысл лишь совокупность этих полей, представляющая
собой единое электромагнитное поле.
Если поля стационарны, т.е. ![]() и
и ![]() , уравнения Максвелла
приобретают вид:
, уравнения Максвелла
приобретают вид:
![]() ,
,
![]() . (11)
. (11)
В этом случае поля независимы
друг от друга и их можно изучать отдельно.
В дифференциальной форме:
Уравнения (9) и (10) будут
иметь следующий вид:
![]() (12)
(12) ![]() (13)
(13)
Укажем их физический смысл.
Кроме того, эти уравнения не только выражают основные законы электромагнитного
поля, но и позволяют при их интегрировании найти сами поля ![]() и
и ![]() .
.
В интегральной форме уравнения Максвелла
являются более общими, т.к. они справедливы на границе сред. Дифференциальная
форма имеет ограниченность – все величины в пространстве и времени изменяются
только непрерывно. Поэтому они
дополняются граничными условиями:
![]() (14)
(14)
и материальными уравнениями: ![]() . (15)
. (15)
Свойства уравнений Максвелла:
1)Уравнения Максвелла линейны,
т.е. содержат только первые производные ![]() и
и ![]() по координатам и времени и первые степени ρ и j.
по координатам и времени и первые степени ρ и j.
2)Они содержат уравнение
непрерывности т.е. закон сохранения электрического заряда.
3)Выполняются во всех ИСО,
т.е. являются релятивистски инвариантными.
4)Не являются симметричными
относительно электрического и магнитного полей из-за отсутствия магнитных
зарядов в природе. Но в нейтральной однородной непроводящей среде, где ρ=0
и j=0 уравнения Максвелла становятся симметричными (исключая знак):
![]()
![]() . (16)
. (16)
Если
электрические и магнитные поля стационарны (dD/dt = dB/dt = 0), то эти поля
существуют независимо друг от друга. Электрическое поле описывается двумя
уравнениями электростатики : rot E = 0 и div D = p, а магнитное поле - двумя
уравнениями магнитостатики : rot H = j
и div B = 0;
6 Особое
место занимают гармонические колебания по
2-м причинам: а) колебания в природе и технике близки к гармоническим, б)
другие периодические колебания можно выразить как суперпозицию нескольких
гармонических.
8. Гармонические колебания и их характеристики. Дифференциальное уравнение гармонических колебаний.
Гармонические колебания
Это – колебания по закону
синуса или косинуса.
Уравнение движения: ![]() или при одномерном
движении:
или при одномерном
движении: ![]()
Далее
![]() или
или ![]() . (1)
. (1)
Это
– однородное дифференциальное уравнение 2-го порядка.
Здесь ![]() . Решение ищется в
виде:
. Решение ищется в
виде: ![]() .
.
В
итоге общее решение получается в виде:
![]() . (2)
. (2)
А –
амплитуда (наибольшее смещение); α – начальная фаза; ![]() - фаза.
- фаза.
Связь периода Т и частот ν и ω : ![]() ,
, ![]() ,
, ![]() . (3)
. (3)
График
x=f(t) имеет вид:
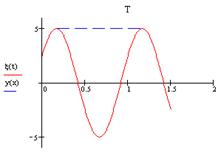
Продифференцировав
(2) по времени, получим скорость:
![]() (4)
(4)
Т.О. скорость опережает
смещение х по фазе на π/2.
Вторая производная даст
ускорение:
![]() . (5)
. (5)
Ускорение
и смещение находятся в противофазе.
Колебание
известно, если известны А и α. Они определяются из начальных условий:
значений х0, v0 при t = 0.
![]() ,
, ![]() . Решая совместно,
получим:
. Решая совместно,
получим:
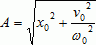 ,
, ![]() . (6)
. (6)
9. Гармонические осцилляторы. Энергия гармонических колебаний пружинного маятника.
7 Энергия гармонических колебаний
Из
механики известно, что квазиупругая сила ![]() является консервативной, поэтому полная энергия гармонических
колебаний должна оставаться постоянной. При колебаниях происходит превращение Ер
в Ек и обратно.
является консервативной, поэтому полная энергия гармонических
колебаний должна оставаться постоянной. При колебаниях происходит превращение Ер
в Ек и обратно.
При х = А
![]() . (7)
. (7)
При х = 0
![]() . (8)
. (8)
Зависимость их от времени
определяется выражениями:
![]() .
. ![]() .
.
Полная энергия:
![]() . (9)
. (9)
Т.О.
полная энергия действительно остается постоянной.
Используя
тригонометрические соотношения:
![]() и
и ![]() ,
,
получим,
что Ек и Ер изменяются с частотой 2ω.
8 Пружинный маятник- это груз массой m,
подвешенный на абсолютно упругой пружине и совершающий гармонические колебания
под действием упругой силы ![]()

формула
периода справедлива , когда масса пружины мала по сравнению с массой тела
Потенциальная
энергия пружинного маятника: ![]()
11. Векторная диаграмма. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения.
9 Векторная диаграмма.
Возьмем
ось Х. Из точки О отложим вектор длины А под углом α к оси Х и будем его
вращать с угловой скоростью ω0. Тогда проекция конца вектора
будет перемещаться вдоль х от –А до +А, а координата проекции будет изменяться
со временем по закону:
![]() ,
,
т.е. будет совершать
гармоническое колебание с амплитудой А, равной длине вектора, круговой
частотой, равной угловой скорости вращения вектора, и начальной фазой, равной
углу α между вектором и Х в начальный момент времени. Другими словами
гармонические колебания можно изображать с помощью векторов.
Сложение колебаний одинакового направления.
Запишем 2 колебания вдоль оси
Х:
![]() и
и ![]()
Из рис.2 видно, что х = х1
+ х2
и
![]() (10)
(10)
![]() . (11)
. (11)
Биения
При сложении двух гармонических колебаний
одинакового направления, мало отличающихся по частоте возникают биения. Их можно рассматривать как
гармоническое колебание с пульсирующей амплитудой. По условию
![]()
![]() и
и ![]()
Результирующее колебание:
![]() (12),
(12),
где амплитуда = ![]() , т.к. она не может быть отрицательной.
, т.к. она не может быть отрицательной.
Частоту пульсаций амплитуды
называют частотой биений и она равна ![]() .
.
12. Сложение взаимно перпендикулярных гармонических колебаний. Фигуры Лиссажу.
10 Сложение взаимно-перпендикулярных колебаний
Примем начальную фазу 1-го колебания
равной 0. Тогда
![]() и
и ![]() , (1)
, (1)
где ![]() - разность фаз обоих
колебаний.
- разность фаз обоих
колебаний.
Для получения траектории исключим параметр
t.
![]() . Тогда
. Тогда ![]() . (2)
. (2)
и
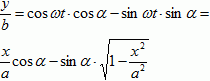 .
.
После преобразований получим:
![]() . (3)
. (3)
Уравнение эллипса. Исследуем
форму траектории в зависимости от разности фаз и амплитуд.
1) ![]() . Тогда (3):
. Тогда (3):
![]() или
или ![]() . (4)
. (4)
Точка колеблется вдоль
прямой ![]() , (5)
, (5)
полученной из (1) с учетом
того, что ![]() . Вывод ?
. Вывод ?
2) ![]() . Тогда (3) примет вид:
. Тогда (3) примет вид:
![]() , откуда
, откуда ![]() . (4/)
. (4/)
3) ![]() . Тогда получим
эллипс:
. Тогда получим
эллипс: ![]() . (5)
. (5)
Если ![]() , то эллипс вырождается в окружность.
, то эллипс вырождается в окружность. ![]() дает разные направления (анализ следует из (1), + соответствует
движению по часовой стрелке.
дает разные направления (анализ следует из (1), + соответствует
движению по часовой стрелке.
Фигуры Лиссажу
1) При ![]() и
и ![]() получим уравнения
колебаний:
получим уравнения
колебаний:
![]() ,
, ![]() .
.
Пока
вдоль ОХ точка смещается из одного крайнего положения в другое, вдоль оси ОУ,
выйдя из нулевого положения, она успевает достигнуть одного крайнего, затем
другого и вернуться в нулевое (исходное) положение.
2)
При ![]() и
и ![]() получаем незамкнутую
кривую, по которой движется точка туда и обратно.
получаем незамкнутую
кривую, по которой движется точка туда и обратно.
Чем ближе к
единице дробь, тем сложнее фигура
Лиссажу.
3) Рассмотрим ![]() и
и ![]() .
.
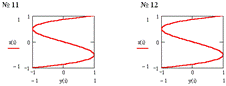
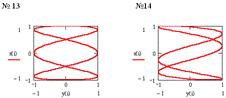
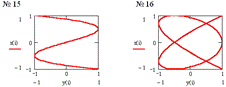
Фигуры Лиссажу
- замкнутые траектории точки М, одновременно совершающей гармонические
колебания в двух взаимно-перпендекулярных направлениях. Форма фигур зависит от
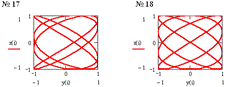
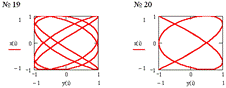
соотношения амплитуд, частот и начальных фаз складываемых колебаний:![]() , где p и q
- целые числа. Значения координат колеблющейся точки М одновременно повторяются
через одинаковые промежутки времени Т0 , равные общему наименьшему кратному
, где p и q
- целые числа. Значения координат колеблющейся точки М одновременно повторяются
через одинаковые промежутки времени Т0 , равные общему наименьшему кратному![]() - периодов
колебаний вдоль осей ОХ и ОУ. Отношение частот
- периодов
колебаний вдоль осей ОХ и ОУ. Отношение частот![]() равно
отношению числа касаний соответствующей им фигуры Лиссажу со стороной
прямоугольника, параллельной оси ОУ, и со стороной, параллельной оси ОХ. В
таблице приведены параметры соответствующих, представленных ниже на рисунках системы
MathCAD, 20 фигур Лиссажу.
равно
отношению числа касаний соответствующей им фигуры Лиссажу со стороной
прямоугольника, параллельной оси ОУ, и со стороной, параллельной оси ОХ. В
таблице приведены параметры соответствующих, представленных ниже на рисунках системы
MathCAD, 20 фигур Лиссажу. 




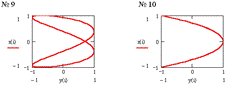
10. Свободные гармонические колебания в колебательном контуре. Собственная частота контура. Формула Томсона.
11 Колебательным называется контур, состоящий
из катушки индуктивности L и конденсатора
С, в котором могут возникнуть электрическое колебания (рис.1). Рассмотрим этот
процесс: Пусть верхняя обкладка С заряжена положительно. Вся энергия заключена
в С. При замыкании ключа, С разряжается, через L течет ток. Электрическая энергия С переходит в магнитную энергию
катушки (через ![]() ), далее ток убывает (не сразу с учетом явления
самоиндукции), а положительный заряд переходит на нижнюю обкладку С (через
следующие
), далее ток убывает (не сразу с учетом явления
самоиндукции), а положительный заряд переходит на нижнюю обкладку С (через
следующие ![]() ), т.е. через полпериода энергия вновь полностью переходит в
электрическую. С этого момента С вновь начнет разряжаться, ток потечет в
обратном направлении и т.д. – процесс будет повторяться.
), т.е. через полпериода энергия вновь полностью переходит в
электрическую. С этого момента С вновь начнет разряжаться, ток потечет в
обратном направлении и т.д. – процесс будет повторяться.
При ![]() (активное
сопротивление контура) происходят строго периодические колебания. При
(активное
сопротивление контура) происходят строго периодические колебания. При ![]() часть энергии переходит в тепло, будут затухающие колебания.
часть энергии переходит в тепло, будут затухающие колебания.
Получим общее уравнение колебательного
контура, содержащего последовательные С, L, R и внешнюю переменную ЭДС ![]() . (Рис.2).
. (Рис.2).
Выберем положительное
направление обхода и соответствующий ему переход заряда. Тогда
![]() . (1)
. (1)
Для участка 1RL2 по закону Ома
![]() . (2)
. (2)
Здесь
![]() и
и ![]() .
.
Тогда (2) перепишем в виде
![]() или
или ![]() . (3)
. (3)
Чаще пишут уравнение
колебательного контура в виде
![]() (4)
(4)
где
![]() (или
(или ![]() ) и
) и ![]() . (5)
. (5)
Если ![]() , колебания называются ?
, колебания называются ?
Если ![]() , колебания называются ?
, колебания называются ?
Если ![]() , колебания называются ?
, колебания называются ?
13. Затухающие колебания и их характеристики. Дифференциальное уравнение затухающих колебаний.
12 Свободные затухающие колебания
Здесь ![]() и
и ![]() . Тогда дифференциальное
уравнение
. Тогда дифференциальное
уравнение
![]() . (12)
. (12)
При слабом затухании (![]() ) решение имеет вид
) решение имеет вид
![]() , (13)
, (13)
где
![]() . (14)
. (14)
Период
затухающих колебаний:
 . (15)
. (15)
Амплитуда = ![]()
Напряжение на С: ![]() . (16)
. (16)
Ток в контуре:

Преобразуем выражение в
скобках к косинусу. Умножим и разделим его на
![]() и введем угол ψ по формулам
и введем угол ψ по формулам ![]() ,
,![]() . (17)
. (17)
Тогда можно получить выражение
![]() (18)
(18)
Из (17): угол ψ лежит во
2-й четверти (![]() ), т.е. ток опережает по фазе напряжение UC более чем на
), т.е. ток опережает по фазе напряжение UC более чем на ![]() . Характеристики
затухающих колебаний
. Характеристики
затухающих колебаний
а) Коэффициент затухания ![]() и время релаксации
и время релаксации ![]()
![]() - время, за которое амплитуда колебаний убывает в е = 2,72
раз.
- время, за которое амплитуда колебаний убывает в е = 2,72
раз.
![]() (19), при
(19), при ![]()
![]() . Тогда
. Тогда ![]() или
или ![]() . (20)
. (20)
б) Логарифмичекий
декремент затухания![]()
По определению
![]() . (21)
. (21)
или
![]() . (22)
. (22)
Ne – число колебаний за
время τ.
При слабом затухании (![]() ) имеем
) имеем ![]() , тогда
, тогда
![]() . (23)
. (23)
в) Добротность
Q колебательного контура
По определению
![]() . (24)
. (24)
При слабом затухании (![]() ) добротность контура равна
) добротность контура равна
![]() (25)
(25)
И
![]() , (26)
, (26)
где W- энергия, запасенная в контуре, δW – уменьшение этой энергии за период колебаний. (26) показать самим.
Если ![]() вместо колебаний получим апериодический разряд конденсатора.
Активное сопротивление контура при наступлении этого процесса (
вместо колебаний получим апериодический разряд конденсатора.
Активное сопротивление контура при наступлении этого процесса (![]() ) называется критическим.
) называется критическим.
![]() . (27)
. (27)
14. Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний. Частота, амплитуда и фаза вынужденных колебаний. Резонанс.
13 Установившиеся колебания. Амплитуда и фаза
вынужденных колебаний.
В
уравнении колебательного контура учтем
внешнюю переменную ЭДС ![]() , зависящую от времени по гармоническому закону:
, зависящую от времени по гармоническому закону:
![]() . (1)
. (1)
Отметим,
что в колебательном контуре сохраняется гармонический характер колебаний при
действии внешней гармонической ЭДС.
Теперь уравнение примет вид:
![]() (2)
(2)
или
![]() . (3)
. (3)
Решение
состоит из общего решения однородного и частного решения неоднородного
уравнения.
Для установившихся колебаний важным
является только частное решение неоднородного (почему ?):
![]() , (4)
, (4)
где
![]() - амплитуда заряда на С;
- амплитуда заряда на С; ![]() - разность фаз между колебаниями заряда и внешней ЭДС. Обе
эти величины определяются только свойствами самого контура и вынуждающей ЭДС,
причем, как увидим позже,
- разность фаз между колебаниями заряда и внешней ЭДС. Обе
эти величины определяются только свойствами самого контура и вынуждающей ЭДС,
причем, как увидим позже, ![]() , поэтому q всегда отстает
по фазе от
, поэтому q всегда отстает
по фазе от ![]() .
.
Для определения ![]() и
и ![]() можно подставить (4) в (2) и преобразовать выражение. Для
простоты мы поступим по-другому: сначала найдем ток и подставим его в (3).
можно подставить (4) в (2) и преобразовать выражение. Для
простоты мы поступим по-другому: сначала найдем ток и подставим его в (3).
Итак

Перепишем
его в виде
![]() . (5)
. (5)
Здесь ![]() - амплитуда тока;
- амплитуда тока; ![]() - сдвиг по фазе между током и внешней ЭДС.
- сдвиг по фазе между током и внешней ЭДС.
![]() и
и ![]() . (6)
. (6)
Задача
состоит в определении ![]() и
и ![]() . Для этого ур.(3) представим в виде:
. Для этого ур.(3) представим в виде:
![]() .
.
С
учетом (6) можно записать:
![]() , (7)
, (7)
 , (8)
, (8)
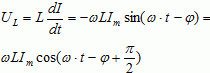 . (9)
. (9)
Видно,
что UR находится в фазе с током, UC отстает по фазе от тока на ![]() , а UL опережает ток
на
, а UL опережает ток
на ![]() .
.
Теперь используем векторную диаграмму для
амплитуд напряжений:
![]() ,
, ![]() ,
, ![]()

 ;
; 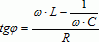
Резонанс и резонансные кривые
Резонанс – явление возникновения сильных
колебаний в контуре при частоте внешней ЭДС (или напряжения), равной или
близкой к собственной частоте.
Используется в радиотехнике для выделения
из сложного напряжения нужной составляющей. Путем изменения параметров C и L колебательного
контура добиваются совпадения его собственной частоты с частотой
электромагнитных волн, излучаемых радиостанцией.
С явлением резонанса связана и опасность:
внешние ЭДС или напряжение могут быть малыми, но напряжение на С или L могут достигать опасного для жизни человека значения.
К резонансным кривым относятся зависимости
от частоты: 1)тока I, 2) заряда q, 3-5) напряжений UR, UL, UC.
Покажем полученный в МатКАДе резонанс
тока, напряжений, мощности, заряда.


 114
114
15. Переменный электрический ток как вынужденные колебания. Условие квазистационарности. Закон Ома для переменного тока.
Переменный эл
ток. З-н Ома для переменного тока
для
переменного тока, мгновенные значения во всех сечениях цепи практически
одинаковы, т.к. их изменения происходят достаточно медленно, а эл/магн
возмущения распространяются по цепи со скоростью света.
![]()
Переменный
ток, текущий через резистор сопротивлением R
З-н
Ома: ![]() , где
амплитуда силы тока
, где
амплитуда силы тока ![]()
Сдвиг
фаз м/у ![]() и
и![]() равен нулю
равен нулю
Переменный
ток, текущий ч/з катушку индуктивностью L
Если
в цепи приложено переменное напряжение![]() , то в ней
потечет переменное ток, в рез-те чего возникает переменная эдс самоиндукции
, то в ней
потечет переменное ток, в рез-те чего возникает переменная эдс самоиндукции ![]() . з-н Ома:
. з-н Ома: ![]() откуда
откуда ![]() . Т.к.
внешнее напряжение приложено к катушке индуктивности, то
. Т.к.
внешнее напряжение приложено к катушке индуктивности, то ![]() - падение
напряжение на катушке
- падение
напряжение на катушке![]() , где
, где ![]()
![]() - падение
напряжения опережает по фазе ток, текущий ч/з катушку, на
- падение
напряжения опережает по фазе ток, текущий ч/з катушку, на ![]()
Переменный
ток, текущий ч/з конденсатор емкостью С
![]()
![]() , где
, где ![]()
падение
напряжения на конденсаторе ![]() отстает по
фазе от текущего ч/з конденсатор тока I на
отстает по
фазе от текущего ч/з конденсатор тока I на ![]()
Цепь
переменного тока, содержащая последовательно включенные резистор, катушку
индуктивности и конденсатор
Разность
фаз м/у напряжением и силой тока: ![]()
Амплитуда
силы тока: 
Если
напряжение в цепи меняется по з-ну![]() , то в цепи
течет ток
, то в цепи
течет ток![]()
Полное сопротивление цепи: ![]()
Установившиеся вынужденные колебания можно
рассматривать как протекание в цепи, обладающей емкостью С, индуктивностью L и
активным сопротивлением R, переменного тока. Под действием внешнего напряжения
![]() ток в цепи
изменяется по закону
ток в цепи
изменяется по закону![]() где
где
 Квазистационарным
называется ток, мгновенные значения которого являются практически одинаковыми
на всех участках цепи. Приведем графики зависимости напряжения и силы тока от
времени, выражаемые формулами (1) и (2).
Квазистационарным
называется ток, мгновенные значения которого являются практически одинаковыми
на всех участках цепи. Приведем графики зависимости напряжения и силы тока от
времени, выражаемые формулами (1) и (2). 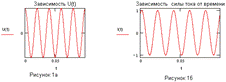 Итак, решение задачи сводится к определению
величин, определяемых выражениями (3), т.е. амплитуды силы тока Im и сдвига
тока по фазе
Итак, решение задачи сводится к определению
величин, определяемых выражениями (3), т.е. амплитуды силы тока Im и сдвига
тока по фазе ![]() относительно
напряжения U. Первую формулу в (3) можно понимать как закон Ома для амплитудных
значений тока и напряжения. В общем случае закон Ома записывается для любых
мгновенных значений этих величин: I = U/Z,где
относительно
напряжения U. Первую формулу в (3) можно понимать как закон Ома для амплитудных
значений тока и напряжения. В общем случае закон Ома записывается для любых
мгновенных значений этих величин: I = U/Z,где
![]() Z называют импедансом или полным
сопротивлением цепи. Видно, что при
Z называют импедансом или полным
сопротивлением цепи. Видно, что при ![]() сопротивление
минимально и равно активному сопротивлению : Z = R. Величина
сопротивление
минимально и равно активному сопротивлению : Z = R. Величина ![]() называется
реактивным сопротивлением, ее можно представить в виде
называется
реактивным сопротивлением, ее можно представить в виде ![]() представляет
собой индуктивное сопротивление, а
представляет
собой индуктивное сопротивление, а ![]() емкостное
сопротивление. Тогда импеданс можно записать как
емкостное
сопротивление. Тогда импеданс можно записать как ![]() .
.
Средняя (за период) мощность
переменного тока равна![]() где cos
где cos ![]() -
коэффициент мощности, равный отношению R/Z;
-
коэффициент мощности, равный отношению R/Z; ![]() -
действующие или эффективные значения напряжения и силы тока. Мощность можно
также выразить как
-
действующие или эффективные значения напряжения и силы тока. Мощность можно
также выразить как
![]()
Такую же мощность развивает
постоянный ток с силой тока ![]() . Все
заводские и лабораторные амперметры и вольтметры проградуированы по действующим
значениям тока и напряжения.
. Все
заводские и лабораторные амперметры и вольтметры проградуированы по действующим
значениям тока и напряжения.
Условие
квазистационарности:
![]() . (1)
. (1)
При выполнении условия (1)
можно использовать законы постоянного тока, например, закон Ома, правила
Кирхгофа и т.д.
16. Мгновенная и средняя мощность, выделяемая в цепи переменного тока. Коэффициент мощности.
15 Работа и мощность
переменного тока
мгновенное
значение мощности переменного тока ![]() , где
, где ![]()
![]()
![]()
![]() - среднее
значение за период колебаний
- среднее
значение за период колебаний
![]()
Такую
же мощность развивает постоянный ток ![]() - действующие значения тока и напряжения.
- действующие значения тока и напряжения.
![]() , где
, где ![]() -
коэффициент мощности.
-
коэффициент мощности.
Мощность,
выделяемая цепи переменного тока, зав-ит не только от силы тока и напряжения,
но и от сдвига фаз м/у ними. Если в цепи реактивное сопротивление отсутствует,
то ![]() и
и ![]()
Если
цепь содержит только реактивное сопротивление (R=0), то ![]() и средняя мощность равна нулю.
и средняя мощность равна нулю.
17. Волны в упругой среде. Основные характеристики волн (частота, длина волны, фазовая скорость, волновое число). Уравнения плоской и сферической синусоидальных волн.
16 Волной называется процесс распространения колебаний в пространстве.
Волны могут распространяться в
любой среде. Колебания передаются из-за взаимодействия между частицами среды,
но сами частицы не перемещаются вместе с волной.
Волны бывают продольными, когда частицы колеблются в направлении волны, и поперечными, когда колебания частиц
перпендикулярны. Продольные волны возникают в любой среде, поперечные – только
в твердых и на границе жидкой и газообразной сред.
Рассмотрим механизм образования поперечной
волны на рис.1.
Продольная волна представляет
собой чередующиеся сгустки и разрежения.
Фронт
волны- геометрическое место точек, до которых доходят колебания в момент
времени t. Он всегда один!
Волновая
поверхность - геометрическое место
точек, колеблющихся в одинаковой фазе. Их бесконечное множество!
Волны бывают плоскими,
сферическими, цилиндрическими и т.д. в зависимости от формы волной
поверхности.
На рис. 2 показана зависимость смещения ![]() точек от положения
точек от положения ![]() этих точек в некоторый
момент времени.
этих точек в некоторый
момент времени.
Длина
волны – расстояние, на которое распространяется волна за период колебаний,
или это – расстояние между точками среды, разность фаз колебаний которых
составляет ![]() .
.
λ = vT, (1)
отсюда с учетом ![]() получим
получим
v = λν. (2)
Уравнение плоской волны
Это – выражение зависимости
смещения ξ от координат x,y,z и времени t:
![]() ,
,

являющееся периодической
функцией относительно координат и времени.
Найдем вид ![]() для плоской волны вдоль оси х.
для плоской волны вдоль оси х.
Тогда ![]() . Для точек, находящихся
в плоскости х = 0, запишем:
. Для точек, находящихся
в плоскости х = 0, запишем:
![]() .
.
Для точек в плоскости с
произвольным значением х:
Рис.3
 .
.
Уравнение плоской (продольной
или поперечной) волны:
![]() . (3)
. (3)
Зафиксируем фазу
![]()
Возьмем дифференциал:
![]() ,
,
откуда ![]() -скорость распространения фазы волны или фазовая скорость
-скорость распространения фазы волны или фазовая скорость
Введем величину
![]() . (4)
. (4)
Это-волновое число,
показывающее, сколько длин волн умещается на длине ![]() . Преобразуем (4) к виду
. Преобразуем (4) к виду
![]() . (5)
. (5)
С учетом (5) уравнение плоской
волны можем записать в виде:
![]() (6)
(6)
Уравнение сферической волны
![]() (7)
(7)
18. Волновое уравнение для упругих волн. Фазовая скорость.
Волновое уравнение
Найдем дифференциальное
уравнение волны, называемое волновым.
Уравнения (6) и (7) являются его решением. Обобщим уравнение (6) для произвольного
направления.
![]() . (6/)
. (6/)
Или
![]() (6//).
(6//).
Вторые производные данной
функции дают:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Сложим 3 последних уравнения:
 .Вместо
.Вместо ![]() подставим его
выражение из 1-й формулы и с учетом
подставим его
выражение из 1-й формулы и с учетом
![]()
Получим волновое уравнение:
![]() . (7)
. (7)
или
![]() . (7/)
. (7/)
17 Если среда, в к-ой распространяется одновременно нес-ко волн, линейна,
т.е. ее св-ва не изменяются под действием возмущений, создаваемых волной, то к
ним применим принцип суперпозиции волн:
при распространении в линейной среде неск-их волн каждая из них
распространяется так, как будто другие волны отсутствуют, а результирующее
смещение частицы среды в любой момент времени равно геометрической сумме
смещений, к-ые получают частицы, участвуют в каждом из слагающих волновых
процессов.
![]() - смещение частицы
среды
- смещение частицы
среды
![]()
![]()
![]()
Результирующее
возмущение в какой-л точке среды = векторной сумме возмущений частиц среды,
вызываемых в данной точке каждой волной по отдельности.
Следствие
суперпозиции – независимость распространения волн
Исходя
из принципа суперпозиции, любой произвольный сигнал (сложная волна) можно
представить в виде группы, суммы синусоидальных волн.
Стоячие
волны.
Стоячие
волны - это волны, образующиеся при наложении двух бегущих волн,
распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами, а в случае поперечных волн и
одинаковой поляризацией.
![]()
Уравнение
стоячей волны: ![]()
В
каждой точке этой волны происходят колебаний той же частоты с амплитудой ![]()
,
зависящей от координаты х рассматриваемой точки.
В
точках среды, где ![]() (m=0,1,2,…),
амплитуда колебаний достигает максимального значения, равного 2А. В точках
среды, где
(m=0,1,2,…),
амплитуда колебаний достигает максимального значения, равного 2А. В точках
среды, где ![]() (m=0,2,3,…), амплитуда колебаний обращается в
ноль.
(m=0,2,3,…), амплитуда колебаний обращается в
ноль.
Точки,
в к-ых амплитуда колебаний максимальна (Аст=2А), наз. пучностями стоячей волны,
а точки, в к-ых амплитуда колебаний равна нулю (Аст=0), наз узлами стоячей
волны. Точки среды, находящиеся в узлам, колебаний не совершают.
19. Энергия упругой волны. Вектор Умова. Интенсивность волны.
18 Энергия упругой волны
Пусть по оси х распространяется плоская продольная волна
![]()
Выделим физически малый объем ![]() , во всех точках которого скорости
, во всех точках которого скорости ![]() и деформации
и деформации ![]() одинаковы.
одинаковы. ![]() обладает кинетической энергией
обладает кинетической энергией
![]() .
.
Потенциальная энергия объема ![]() при упругой деформации
при упругой деформации
![]() .
.
Используем выражение для
скорости: ![]() . Заменим Е через ρV2, тогда
. Заменим Е через ρV2, тогда
![]() .
.
Полная энергия равна
 . (8)
. (8)
Отсюда получим плотность
энергии
![]() . (9)
. (9)
Получим из первого уравнения
![]() ,
,
![]() .
.
Подставим их в выражение для ![]() :
:
![]() . (10)
. (10)
Эта формула справедлива и для
поперечной волны. Среднее по времени значение
в фиксированной точке равно
![]() . (11)
. (11)
Потоком
энергии называется количество энергии,
переносимое волной через поверхность в единицу времени.
![]() . (12)
. (12)
Тогда плотность потока энергии
определяется как
![]() . (13)
. (13)
Через площадку ![]() за время
за время ![]() переносится энергия
переносится энергия ![]() , заключенная в объеме цилиндра с основанием
, заключенная в объеме цилиндра с основанием ![]() и высотой
и высотой ![]() .
.
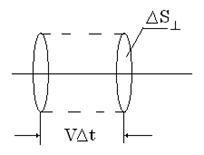
![]() . Подставим в j:
. Подставим в j:
![]() или в векторной форме
или в векторной форме ![]() . (14)
. (14)
Это – вектор Умова.
Среднее значение равно: ![]() . (15)
. (15)
Рис. 4 (15) выражает интенсивность
волны в данной точке.
Зная j, можно определить поток:
![]() . (16)
. (16)
Вычислим среднее значение
потока энергии через произвольную волновую поверхность S незатухающей сферической волны.
![]() .
.
Подставим j из (15):
![]() .
.
Среда не поглощает энергии,
поэтому
![]() (17)
(17)
Отсюда
следует, что амплитуда ![]() незатухающей сферической волны обратно пропорциональны
расстоянию
незатухающей сферической волны обратно пропорциональны
расстоянию ![]() от источника волны.
от источника волны.
19 Эффект Доплера в акустике объясняется тем, что частота колебаний,
воспринимаемых приемником, определяется скоростями движения источника колебаний
и приемника относительно среды, в которой происходит распространение звуковых
волн. Эффект Доплера наблюдается также и при движении относительно друг друга
источника и приемника электромагнитных волн. Так как особой среды, служащей
носителем электромагнитных волн, не существует, то частота световых волн,
воспринимаемых приемником (наблюдателем), определяется только относительной
скоростью источника и приемника (наблюдателя). Закономерности эффекта Доплера
для электромагнитных волн устанавливаются на основе специальной теории относительности.
Теория
относительности приводит к следующей формуле, описывающей эффект Доплера для
электромагнитных волн в вакууме:
 (1)
(1)
Где ![]() - скорость источника
света относительно приемника, с – скорость света в вакууме,
- скорость источника
света относительно приемника, с – скорость света в вакууме, ![]() ,
, ![]() - угол между вектором скорости
- угол между вектором скорости ![]() и направлением
наблюдения, измеряемый в системе отсчета, связанной с наблюдателем.
и направлением
наблюдения, измеряемый в системе отсчета, связанной с наблюдателем.
При ![]() =0:
=0: ![]() (2)
(2)
Эта
формула определяет ек называемый продольный эффект Доплера, наблюдаемый при
движении приемника вдоль линии, соединяющей его с источником. При малых
относительных скоростях ![]() , разлагая (2) в ряд по степеням
, разлагая (2) в ряд по степеням ![]() и пренебрегая членом
порядка
и пренебрегая членом
порядка ![]() , получим
, получим ![]() .(3)
.(3)
Следовательно,
при удалении источника и приемника друг от друга(при их положительной
относительной скорости) наблюдается сдвиг в более длинноволновую область (![]() )-так называемое красное
смещение. При сближении же источника и приемника (при их отрицательной
относительной скорости) наблюдается сдвиг в более коротковолновую область (
)-так называемое красное
смещение. При сближении же источника и приемника (при их отрицательной
относительной скорости) наблюдается сдвиг в более коротковолновую область (![]() )- так называемое фиолетовое
смещение.
)- так называемое фиолетовое
смещение.
Если
![]() , то выражение (1) примет вид:
, то выражение (1) примет вид: ![]() (4)
(4)
Формула
определяет поперечный эффект Доплера,
наблюдаемый при движении приемника перпендикулярно линии, соединяющей его с
источником.
20 Из
уравнений Максвелла следуют основные свойства
электромагнитных полей и волн:
1.Электромагнитное поле может
существовать самостоятельно – без
электрических зарядов и токов! Это следует из-за наличия в уравнениях тока
смещения ![]() , т.е. переменного электрического поля, и переменного
магнитного поля
, т.е. переменного электрического поля, и переменного
магнитного поля ![]() . ~ В → ~ Е и наоборот. Такое взаимное превращение
происходит непрерывно, поэтому они сохраняются и распространяются в
пространстве.
. ~ В → ~ Е и наоборот. Такое взаимное превращение
происходит непрерывно, поэтому они сохраняются и распространяются в
пространстве.
2. Изменение состояния поля
обязательно имеет волновой характер,
т.е. распространяющиеся в пространстве поля являются электромагнитными волнами.
3. В вакууме они всегда
распространяются со скоростью с. В
непроводящей неферромагнитной среде
![]() , где
, где ![]() . (1)
. (1)
4.Векторы ![]() взаимно перпендикулярны и образуют правовинтовую систему. Это
– внутреннее свойство
электромагнитной волны (см.рис.1)
взаимно перпендикулярны и образуют правовинтовую систему. Это
– внутреннее свойство
электромагнитной волны (см.рис.1)
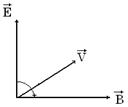
Рис. 1
5.Векторы ![]() всегда колеблются в
одинаковых фазах. Между мгновенными значениями
всегда колеблются в
одинаковых фазах. Между мгновенными значениями ![]() в любой точке имеет место связь:
в любой точке имеет место связь:
![]()
или ![]() (2)
(2)
22. Волновое уравнение для электромагнитного поля. Электромагнитные волны и их свойства.
Волновое уравнение для электромагнитных волн
Факт получения волнового уравнения из
уравнений Максвелла означает само существование электромагнитных волн.
Для
однородной нейтральной (![]() ) и непроводящей (
) и непроводящей (![]() ) среды при постоянных
) среды при постоянных ![]() и
и ![]() запишем:
запишем:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
С учетом этих выражений
перепишем уравнения Максвелла в дифференциальном виде следующим образом:
![]() , (3)
, (3)
![]() , (4)
, (4)
![]() , (5)
, (5)
![]() . (6)
. (6)
Возьмем ротор от обеих частей уравнения (3):
![]() . (7)
. (7)
В правой части поменяем
местами последовательности дифференцирования:
![]() .
.
Подставим в (7) и используем
(5):
![]() . (8)
. (8)
Преобразуем
левую часть: ![]() . Первое слагаемое =0
(см.(6)), а
. Первое слагаемое =0
(см.(6)), а ![]() . Тогда
. Тогда
![]() .
.
или
![]() . (9)
. (9)
![]() . (9/ )
. (9/ )
Аналогично для ![]() :
:
![]() . (10)
. (10)
Уравнения (7) и (8) указывают,
сто электромагнитные поля могут существовать в виде электромагнитных волн с фазовой
скоростью ![]() .
.
21 Плотность
энергии электромагнитного поля равна сумме плотностей для электрического и
магнитного полей (при отсутствии сегнетоэлектриков и ферромагнетиков):
![]() . (11)
. (11)
Учитывая (2), получим, что ![]() для каждого момента времени, тогда
для каждого момента времени, тогда
![]() .Пойнтинг ввел понятие вектора плотности потока энергии:
.Пойнтинг ввел понятие вектора плотности потока энергии:
![]() (12)
(12)
Поток Ф электромагнитной
энергии равен
![]() .
.
Давление и импульс
Давление электромагнитной волны на тело,
на которое она падает возникает в результате воздействия магнитного поля волны
на электрические токи, возбуждаемые электрическим полей той же волны.
Пусть электромагнитная волна падает на
поглощающее тело (среду), т.е. в нем возникает джоулево тепло с объемной
плотностью σЕ2, т.е. ![]() и поглощающая среда
обладает проводимостью. В такой среде электрическое поле волны возбуждает
электрический ток с плотностью
и поглощающая среда
обладает проводимостью. В такой среде электрическое поле волны возбуждает
электрический ток с плотностью ![]() . Тогда на единицу объема среды действует амперова сила
. Тогда на единицу объема среды действует амперова сила ![]() в направлении волны.
Эта сила и вызывает давление электромагнитной волны. Если нет поглощения,
σ = 0 и давления нет. При полном отражении волны давление возрастает
вдвое.
в направлении волны.
Эта сила и вызывает давление электромагнитной волны. Если нет поглощения,
σ = 0 и давления нет. При полном отражении волны давление возрастает
вдвое.
Давление равно: ![]() (13)
(13)
Плотность импульса равна ![]() , что аналогично выражению
, что аналогично выражению ![]() для импульса фотона.
для импульса фотона.
Энергией
эл/магн – сумма эл и магн полей ![]()
Объемная
плотность энергии эл/магн поля: ![]()
![]()
![]()
![]()
![]()
![]()
![]() - вектор
Умова- Пойтинга. Он направлен в сторону распространения эл/магн волны, а его
модуль равен энергии, переносимой эл/магн волной за единицу времени сквозь
единичную площадку, перпендикулярно направлению распространению волны.
- вектор
Умова- Пойтинга. Он направлен в сторону распространения эл/магн волны, а его
модуль равен энергии, переносимой эл/магн волной за единицу времени сквозь
единичную площадку, перпендикулярно направлению распространению волны.
24. Излучение диполя. Волновая зона. Полярная диаграмма направленности излучения диполя. Мощность излучения.
22 Электрический диполь- система из двух равных по величине, но
противоположных по знаку, зарядов, разделенных некоторым расстоянием ![]() .
.
Если он колеблется, то
излучает электромагнитные волны.
Изменение его момента со временем:
![]() . (14)
. (14)
Рассмотрим элементарный диполь. Для него ![]() . В волновой зоне
. В волновой зоне ![]() .
.

Для сферической волны
Em ~ Hm ~![]() .
.
Следовательно,
интенсивность волны
![]() ~
~![]()
обратно пропорциональна
квадрату расстояния от излучателя и зависит от угла θ. Диаграмма излучения
диполя имеет вид (рис.3).
Рис.2

Рис. 3
Мощность излучения N ~ ![]() . Из (14)
. Из (14) ![]() . Тогда
. Тогда
N ~![]() . (15)
. (15)
Усредним по времени
![]() ~
~![]() . (16)
. (16)
Из (14):
![]() ,
,
где а – ускорение колеблющегося
заряда.
Тогда мощность
N ~ q2 a2.
25. Интерференция волн. Временная и пространственная когерентность.
23 Интерференция световых волн
Пусть в одном направлении распространяются
2 световые волны:
![]() и
и ![]()
Тогда
![]() ,
,
где ![]() .
.
Если ![]() , то волны являются когерентными. Когерентными называются волны, у которых
, то волны являются когерентными. Когерентными называются волны, у которых ![]() и постоянна во времени
разность фаз.
и постоянна во времени
разность фаз.
Для некогерентных волн δ непрерывно
изменяется и ее среднее по времени значение = 0, поэтому
![]() или
или ![]() .
.
Для когерентных волн
![]()
![]() . (1)
. (1)
Явление перераспределения
светового потока в пространстве, в
результате чего в одних местах возникают максимумы интенсивности, а в других -
минимумы, называется интерференцией.
Пример: Пусть ![]() . Из (1) следует:
. Из (1) следует: ![]() .Все естественные
источники света некогерентны.
Объяснение: Излучение тел состоит из волн, испускаемых многими атомами.
Каждый атом излучает цуг волн продолжительностью
.Все естественные
источники света некогерентны.
Объяснение: Излучение тел состоит из волн, испускаемых многими атомами.
Каждый атом излучает цуг волн продолжительностью ![]() с и протяженностью
с и протяженностью ![]() = 3 (м). Через τ
излучение одной группы атомов сменяется излучением другой группы. Фазы разных
цугов даже от одних атомов между собой не связаны, т.е. меняются случайным
образом, так что при усреднении
= 3 (м). Через τ
излучение одной группы атомов сменяется излучением другой группы. Фазы разных
цугов даже от одних атомов между собой не связаны, т.е. меняются случайным
образом, так что при усреднении ![]() .
.
Как же в таком случае можно вообще
наблюдать интерференцию? Проблема
решается просто! Нужно путем отражений или преломлений разделить одну волны
на 2 или более волн, которые после прохождения разных оптических длин путей
следует вновь наложить друг на друга. Тогда наблюдается интерференция.
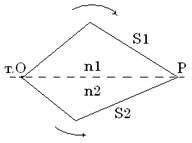
Разделим в т.О (рис.2) волну на две
когерентные. В т.О фаза равна ![]() ,
,
в т. Р фаза 1-й волны: ![]() , a
, a
2-й волны: ![]() . Тогда разность фаз двух колебаний в точке наблюдения Р
будет равна:
. Тогда разность фаз двух колебаний в точке наблюдения Р
будет равна:
![]() .
.
Рис. 2 Заменим ![]() на
на ![]() , тогда получим:
, тогда получим:
![]() , (2)
, (2)
где
![]() (3) - оптическая
разность хода.
(3) - оптическая
разность хода.
Если
![]() , (4)
, (4)
где ![]() , то δ является кратной 2π и колебания, возбуждаемые
в т.Р обеими волнами, будут происходить с одинаковой фазой и усиливают друг
друга , т.е. (4) выражает условие
максимума..
, то δ является кратной 2π и колебания, возбуждаемые
в т.Р обеими волнами, будут происходить с одинаковой фазой и усиливают друг
друга , т.е. (4) выражает условие
максимума..
Условие
минимума:
![]() (5)
(5)
при ![]() , т.е. на разности хода укладывается нечетное число полуволн
в вакууме и колебания в т.Р обеих волн находятся в противофазе.
, т.е. на разности хода укладывается нечетное число полуволн
в вакууме и колебания в т.Р обеих волн находятся в противофазе.
Под когерентностью подразумевается согласованное протекание
колебательных или волновых процессов. При этом степень согласованности может
быть различной.
Различают временную и пространственную
когерентность.
Временная
когерентность определяется разбросом частот Δω или
разбросом значений модуля волнового
вектора k, так как
![]() .
.
Пространственная же связана с разбросом направлений
вектора ![]() .
.
 При
рассмотрении временной когерентности большую роль играет время срабатывания прибора tприб.
Если за tприб cosδ принимает все значения от -1 до +1, то
При
рассмотрении временной когерентности большую роль играет время срабатывания прибора tприб.
Если за tприб cosδ принимает все значения от -1 до +1, то ![]() ; если за tприб
; если за tприб ![]() , то прибор фиксирует интерференцию и волны когерентны. Вывод: Когерентность – понятие
относительное. Волны, когерентные при наблюдении прибором с малым tприб , могут
быть некогерентными при приборе с большим tприб.
, то прибор фиксирует интерференцию и волны когерентны. Вывод: Когерентность – понятие
относительное. Волны, когерентные при наблюдении прибором с малым tприб , могут
быть некогерентными при приборе с большим tприб.
Для характеристики когерентных свойств
волн вводится понятие времени
когерентности ![]() . Это – время, за которое изменение фазы волны достигает
значения ~π. Теперь можно ввести
. Это – время, за которое изменение фазы волны достигает
значения ~π. Теперь можно ввести
критерий
когерентности:
tприб
«![]() . (6)
. (6)
Длина
когерентности(длина цуга) - ![]() . (7)
. (7)
Это – расстояние, на котором
изменение фазы волны достигает значения ~π.
Для получения интерференционной картины
путем деления световой волны на две необходимо, чтобы ![]() . Это требование ограничивает наблюдаемое число
интерференционных полос. Расчеты дают следующие соотношения:
. Это требование ограничивает наблюдаемое число
интерференционных полос. Расчеты дают следующие соотношения:
![]() ~
~ ![]() ~
~ ![]() . (8)
. (8)
![]() ~
~ ![]() . (9)
. (9)
При рассмотрении пространственной
когерентности критерий записывается в виде:
![]() , (10)
, (10)
где φ - угловой размер
источника, d – его линейный размер.
 При смещении вдоль волновой поверхности, излучаемой
источником, расстояние, на котором фаза меняется не более чем на π,
называется длиной пространственной
когерентности или радиусом когерентности:
При смещении вдоль волновой поверхности, излучаемой
источником, расстояние, на котором фаза меняется не более чем на π,
называется длиной пространственной
когерентности или радиусом когерентности:
![]() ~
~![]() . (11)
. (11)
Для солнечных лучей (φ ~
0,01 рад, λ ~ 0,5 мкм. Тогда ![]() =
=
26. Способы наблюдения интерференции света. Оптическая разность хода. Условия максимума и минимума при интерференции.
Способы наблюдения интерференции
Принцип наблюдения интерференции от
естественных источников мы уже рассмотрели. Используются зеркала Френеля
(рис.3), бипризма Френеля (рис.5).
Расчеты для них во многих учебниках имеются.
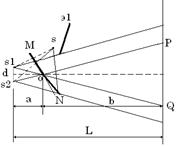
Рис.3
Рассмотрим подробнее
интерференцию в тонких пленках.
На рис.4 разность хода лучей 1
и 2 в точке С равна:
![]() . (12)
. (12)
Видно, что S1 = ВС; S2 = AO + OC;
КС = b* tgβ ; Тогда
![]() и
и ![]() .
.
Рис. 4
Подставим их в (12):
![]() .
.
Сделаем замену
![]() .
.
Получим
![]() .Подставив последнее выражение в Δ, получим
.Подставив последнее выражение в Δ, получим
![]() .
.
При отражении луча 1 в точке С от
оптически более плотной среды фаза изменяется на π. Окончательное
выражение для разности хода:
![]() . (13)
. (13) ![]()
Условия когерентности: Δ ‹ ℓ КОГ, т.е.
![]() ,
,
или
![]() .
.
Тогда
![]() . (14)
. (14)
Таким образом, отраженные
волны будут когерентными только при выполнении условия (14), т.е. когда
удвоенная толщина пластины меньше длины когерентности.
Пример:
![]() ,
, ![]() А. Тогда
А. Тогда ![]() А = 0,06 (мм)
А = 0,06 (мм)
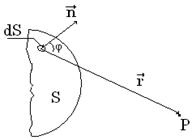
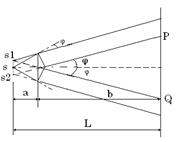
Рис. 5 Бипризма Френеля
27. Дифракция волн. Принцип Гюйгенса – Френеля. Метод зон Френеля.
24 Под дифракцией понимают явления,
наблюдаемые при распространении света в среде с резкими неоднородностями. В
частности, наблюдается огибание световыми волнами препятствий и проникновение
света в область геометрической тени.
Условие дифракции: d ~ λ.
Дифракция, как и
интерференция, проявляется в
перераспределении светового потока при наложении когерентных волн. Различие: при интерференции
рассматривается конечное число источников света, при дифракции – непрерывно
расположенные.
Схема наблюдения дифракции: источник - непрозрачная преграда - экран.
Два вида дифракции: Френеля для сферических волн, Фраунгофера – для плоских.
Принцип Гюйгенса-Френеля
Принцип Гюйгенса
объясняет проникновение света в область тени, но не дает сведений об амплитуде
волн. Согласно принципу Г-Ф учет амплитуд и фаз вторичных волн при их
интерференции позволяет найти амплитуду результирующей волны в любой точке.
От каждого участка dS волновой поверхности
S в точку Р приходит колебание
![]() (1)
(1)
и для всей поверхности S
![]() (2)
(2)
К(φ) = 1 при φ = 0; К(φ) = 0
при φ = π/2.
Рис. 1
Расчет по (2) –очень сложная
задача, но при определенной симметрии по методу зон Френеля определение
амплитуды сильно упрощается.
Суть метода:
От точечного источника S
распространяется сферическая волна. Волновые поверхности симметричны относительно
SP. Волновую поверхность разобъем на равные по площади
кольцевые зоны так, чтобы расстояния от краев каждой зоны до т. Р отличались на
λ/2. Тогда колебания в т. Р от 2-х соседних зон приходят в противофазе и,
поскольку амплитуды от равных площадей
волновой поверхности считаются одинаковыми (по Френелю), то при четном числе
зон в т. Р будет максимум интенсивности (амплитуды), а при нечетном – максимум.
Метод зон Френеля позволил на основе
волновой теории объяснить закон прямолинейного распространения света.
Рассмотрим 2 примера:
28. Дифракция света на узкой щели. Дифракционная решетка. Формула дифракционной решетки.
25 Дифракция Френеля от круглого отверстия.
 Пусть на пути световой волны находится непрозрачный
экран с круглым отверстием радиуса r0. Для данного случая справедливо соотношение:
Пусть на пути световой волны находится непрозрачный
экран с круглым отверстием радиуса r0. Для данного случая справедливо соотношение:
![]() . (3)
. (3)
Определим из (3) число
открытых зон Френеля: ![]() . (4)
. (4)
Запишем выражение для
амплитуды в т. Р:
![]() . (5)
. (5)
или
 . (5/)
. (5/)
Далее
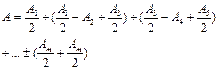
Если m – нечетное, то
![]() . (6) (максимум I)
. (6) (максимум I)
Если m – четное, то
![]() . (7) (минимум I)
. (7) (минимум I)
Дифракция от круглого диска. Здесь всегда в центре максимум.
Первые m зон закрыты, следовательно:

или
![]() . (8)
. (8)
Все формулы справедливы при
малых m.
Рис. 2
Дифракция Фраунгофера на щели
Если на оптической разности
хода укладывается четное число зон Френеля, получим минимум:
![]() , (9)
, (9)
откуда ![]() и
и ![]() . (10)
. (10)
Интенсивность ![]() . (11)
. (11)
Дифракционная решетка
Это – совокупность
одинаковых щелей, отстоящих на одинаковом расстоянии друг от друга. Период(постоянная) решетки – расстояние между серединами соседних щелей.
Схема
на рис.3:
Интенсивность:

Условие min для щели и решетки одинаковы:
![]() , k = 1,2,3…
, k = 1,2,3…
Условие главных
мах:
![]() (12)
(12)
Рис. 3
Условие дополнительных min:
![]() (13)
(13)
где ![]()
Их число равно (N-1) в промежутках между соседними главными максимумами. ![]() принимает все целочисленные значения, кроме 0, N, 2N…
принимает все целочисленные значения, кроме 0, N, 2N…
Число
главных мах равно
![]() . (14)
. (14)
Интенсивность главных мах растет
пропорционально квадрату числа щелей:
![]() . (15)
. (15)
Положение главных максимумов зависит от
λ. Красные лучи, в отличие от дисперсионного спектра, отклоняются сильнее,
чем фиолетовые. Дифракционная решетка работает как спектральный прибор,
разлагая белый свет в спектр.
Угловая дисперсия
![]() .
.
Линейная дисперсия
![]()
Разрешающая способность
![]()
26 Монохроматическая волна вида ![]() представляет собой бесконечную во времени и пространстве
последовательность «горбов» и «впадин», перемещающихся по оси Х с фазовой
скоростью
представляет собой бесконечную во времени и пространстве
последовательность «горбов» и «впадин», перемещающихся по оси Х с фазовой
скоростью ![]() . Но такая волна не может нести полезной информации. Для
этого ее надо оборвать и поместить на ней полезный сигнал. Тогда это уже не
будет монохроматической волной.
. Но такая волна не может нести полезной информации. Для
этого ее надо оборвать и поместить на ней полезный сигнал. Тогда это уже не
будет монохроматической волной.
Проще всего передать сигнал с помощью
светового импульса (см. анимацию). Такой импульс по теореме Фурье можно
представить в виде суперпозиции волн вышеуказанного типа с частотами,
заключенными в некотором интервале ![]() . Группой волн или волновым
пакетом называется суперпозиция волн, мало отличающихся по частоте.
. Группой волн или волновым
пакетом называется суперпозиция волн, мало отличающихся по частоте.
Ее можно выразить в виде
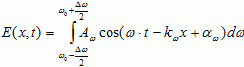 . (18)
. (18)
Для группы волн справедливы
соотношения:
![]() и
и ![]() . (19)
. (19)
 В отсутствие дисперсии (нет зависимости скорости волн
от длины волны или частоты) все плоские волны распространяются с одинаковой
фазовой скоростью V.
Скорость движения группы волн совпадает с V и форма пакета сохраняется. В диспергирующей среде пакет расплывается.
При небольшой дисперсии группе волн можно приписать скорость u перемещения центра пакета или группы волн. Ее называют
групповой скоростью.
В отсутствие дисперсии (нет зависимости скорости волн
от длины волны или частоты) все плоские волны распространяются с одинаковой
фазовой скоростью V.
Скорость движения группы волн совпадает с V и форма пакета сохраняется. В диспергирующей среде пакет расплывается.
При небольшой дисперсии группе волн можно приписать скорость u перемещения центра пакета или группы волн. Ее называют
групповой скоростью.
Напомним ![]() - фазовая скорость. Групповая скорость определяется как
- фазовая скорость. Групповая скорость определяется как
![]() .
.
Последний сомножитель выразим
в виде
![]() .
.
С учетом ![]() получим
получим ![]() .
.
Тогда
![]()
и
![]() .
.
Видно, что в зависимости от
знака ![]() групповая скорость
может быть больше или меньше фазовой скорости V. Групповая скорость равна скорости переноса энергии волной.
групповая скорость
может быть больше или меньше фазовой скорости V. Групповая скорость равна скорости переноса энергии волной.
29. Свет естественный и поляризованный. Способы получения поляризованного света. Законы Малюса и Брюстера.
27 Поглощение и рассеяние света.
Поляризация света. З-ны Малюса и Брюстера
Поглощением
света наз явление уменьшения энергии световой волны при ее распределении в
вещ-ве вследствие преобразования энергии волны в другие виды энергий.
Поглощение света описыв-ся з-ном Бугера: ![]() , где I и
I0 - интенсивность плоской
монохроматической световой волны на входе и выходе слоя поглощающего вещ-ва
толщиной х,
, где I и
I0 - интенсивность плоской
монохроматической световой волны на входе и выходе слоя поглощающего вещ-ва
толщиной х, ![]() -
коэффициент поглащения, зав-ий от длины волны света, хим природы и состояния
вещ-ва и не зав-ей от интенсивности света.
-
коэффициент поглащения, зав-ий от длины волны света, хим природы и состояния
вещ-ва и не зав-ей от интенсивности света.
Свет,
в к-ом направление колебаний светового вектора каким-то образом упорядочены,
наз поляризованным
Степень
поляризации: ![]() , где
I – интенсивность частично поляризованного света, для естественного света
, где
I – интенсивность частично поляризованного света, для естественного света ![]() Р=0, для плоскополяризованного
Р=0, для плоскополяризованного ![]() Р=1
Р=1
З-н
Малюса: ![]() интенсивность прошедшего ч/з пластинку света
изменяется от мин при
интенсивность прошедшего ч/з пластинку света
изменяется от мин при ![]() до макс
до макс
![]()
З-н
Брюстера: ![]() , где
, где ![]() -
показатель преломления 2-ой среды отн-но 1-ой
-
показатель преломления 2-ой среды отн-но 1-ой
28
29
30. Тепловое излучение и его характеристики. Закон Кирхгофа.
31. Понятие абсолютно черного тела. Законы Стефана – Больцмана и Вина.
30, 31 Тепловое
излучение. З-ны теплового излучения. Проблема теплового излучения абсолютно
черного тела.
Тепловое
излучение – эл/магн излучения, обусловленные внутренней энергией тела и
зависящие от температуры и оптич св-в тела
Абсолютно
черное тело - тело, которое полностью поглощает все падающее на него излучение
независимо от направления падающего излучения, его спектрального состава и
поляризации, ничего не отражая и не пропуская. Моделью может служить почти
замкнутая полость (сфера) с небольшим отверстием.
Количественной
х-кой теплового излучения – спектральная плотность энергетической светимости
(излучательность) тела – мощность излучения с единицы площади поверхности тела
в интервале частот единичной ширины
![]() - физ смысл
излучательности (Вт/м2)
- физ смысл
излучательности (Вт/м2)
интегральная
энергетическая светимость  -
интегральная энергетическая светимость
-
интегральная энергетическая светимость
спектральная
поглощательная способность: ![]()
З-н
Кирхгофа: отношение испускательной способности к его поглощательной способности
не зависит от природы тела и равно испускательной способности абсолютно черного
тела при тех же значениях температуры и частоты. ![]()
Физический
смысл: Тело поглащает эл/магн волны преимущественно в том интервале, в к-ом
само их испускает
З-н
Стефана- Больцмана: энергетическая светимость абсолютно черного тела
пропорциональна четвертой степени его абсолютной температуры. ![]()
![]() Вт/м2 К4
Вт/м2 К4
З-н
смещения Вина: длина волны, соотв-ая макс значению спектральной плотности
энергетической светимости черного тела, обратно пропорциональна его
термодинамич температуры ![]()
![]()
мК
Формула
Релея- Джинса: 
32. Проблема излучения абсолютно черного тела. Квантовая гипотеза и формула Планка.
31 Квантовая гипотеза и формула Планка.
Гипотеза
Планка: вещ-во не может испускать энергию излучения иначе как конечными
порциями (квантами), пропорциональными частоте этого излучения
Энергия
кванта равна ![]()
Формула
Планка: 
33. Фотоэффект. Законы фотоэффекта. Уравнение Эйнштейна.
32 Фотоэффект и его з-ны. Ур-е
Эйнштеина
Фотоэффект
– вырывание электронов из атомов или
молекул вещ-ва под действием света (излучения)
Если
электроны, выбитые светом, вылетают за пределы вещ-ва, фотоэффект наз внешним.
Если оторванные электроны остаются внутри освещаемого вещ-ва в качестве
свободных, то фотоэффект наз внутренним.
Скорость
вылетевшего электронов: ![]()
З-ны
Столетова: 1. Сила фотона насыщения пропорциональна световому потоку, падающему
на катод![]() , к –
коэффициент пропорциональности, соотв-ий силе фотона (мкА) при освещении катода
световым потоком 1лм, наз фоточуствительностью освещаемой пластинки
, к –
коэффициент пропорциональности, соотв-ий силе фотона (мкА) при освещении катода
световым потоком 1лм, наз фоточуствительностью освещаемой пластинки
2.
Скорость фотоэлектронов увеличивается с ростом частоты (с уменьшением длины
волны) падающего света и не зав-ит от интенсивности светового потока
3.
Нез-мо от интенсивности светового потока фотоэффект начинается только при
определенной для данного металла мин частоте (макс длине волны) света, наз
красной границей фотоэффекта.
Ур-е
Эйнштейна для внешнего фотоэффекта: ![]() Работа выхода электрона из металла зависит от
природы вещ-ва. С уменьшением частоты падающего света (увеличение длины волны)
энергия падающих квантов (фотонов) при нек-ой частоте (или длине волны) может
стать равной работе выхода,
Работа выхода электрона из металла зависит от
природы вещ-ва. С уменьшением частоты падающего света (увеличение длины волны)
энергия падающих квантов (фотонов) при нек-ой частоте (или длине волны) может
стать равной работе выхода, ![]()
Граничная
длина волны падающего света, при к-ом возникает фотоэффект, наз красной
границей фотоэффекта
34. Фотоны. Энергия и импульс световых квантов. Давление света.
3
33 Фотоны. Энергия и импульс
световых квантов
Фотоны-
элементарная частица, к-ая всегда движется со скоростью света и имеет массу
покоя, равную нулю.
Энергия
фотона: ![]() Масса
фотона:
Масса
фотона: ![]() Импульс
фотона:
Импульс
фотона: 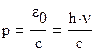
Фотон
как и любая другая частица, х-ся энергией, массой и импульсом
35. Эффект Комптона и его элементарная теория.
34 В ![]() содержатся также лучи большей длины волны
содержатся также лучи большей длины волны ![]() .
Оказалось, что
.
Оказалось, что
![]() (4)
(4)

![]() - угол
рассеяния, т.е. разность
- угол
рассеяния, т.е. разность ![]() от длины волны
от длины волны ![]() и от природы вещества не зависит. Схема опыта
показана на рис. 2.
и от природы вещества не зависит. Схема опыта
показана на рис. 2.
Эффект Комптона объясняется,
представив рассеяние как процесс упругого столкновения рентгеновских фотонов с
почти свободными электронами. Если на первоначально покоящийся свободный
электрон падает фотон с энергией ![]() и импульсом
и импульсом
![]() (рис. 3), то используя законы сохранения
энергии и импульса, можно получить формулу (4).
(рис. 3), то используя законы сохранения
энергии и импульса, можно получить формулу (4).
 где
где
![]() (6)
(6)
носит название комптоновской
длины волны. Определяемая выражением (6) дает для комптоновской длины волны
электрона значение
![]()
36. Линейчатые спектры атомов. Теория атома водорода по Бору. Опыты Франка и Герца.
36 Теория Бора для водородоподобных атомов. Опыты Франка и
Герца.
1
постулат Бора: (постулат стационарных состояний) в атоме существуют
стационарные состояния, в к-ых он не излучает энергии. Стационарным состояниям
атома соответствуют стационарные орбиты, по к-ым движутся электроны. Движение
электронов по стационарным орбитам не сопровождается излучением
электромагнитных волн. В стационарном состоянии атома электрон, двигаясь по
круговой орбите, должен иметь дискретные квантованные значения момента
импульса, удовлетворяющие условию ![]() (n = 1, 2, 3…)
(n = 1, 2, 3…)
2
постулат Бора: (правило частот) при переходе электрона с одной стационарной
орбиты на другую излучается(поглощается) один фотон с энергией ![]() равной разности энергий соответствующих
стационарных состояний. Если
равной разности энергий соответствующих
стационарных состояний. Если ![]() то происходит излучение фотона. Если
то происходит излучение фотона. Если ![]() - поглощение.
- поглощение.
Опыты
Франка и Герца показали, что электроны при столкновении с атомами ртути
передают им только определенные порции энергии (подтверждение идеи Бора). Атомы
ртути, получившие при соударении с электронами энергию ![]() переходят в возбужденное состояние и должны
возвратиться в основное, излучая световой квант.
переходят в возбужденное состояние и должны
возвратиться в основное, излучая световой квант.

37. Гипотеза и формула де Бройля. Опытное обоснование гипотезы де Бройля. Свойства волн де Бройля.
37 Экспериментальные подтверждения
гипотезы и формулы де Бройля
Опыты
Девиссона и Джермерра. При заданном угле падения электроны отражаются от пов-ти
кристалла под различными углами, причем в одних направлениях наблюдаются
максимумы числа отраженных электронов, в других – минимумы, т.е. наблюдалась
диф картина. Это явление наблюдается когда длина электронной волны де Бройля
имеет порядок межатомного расстояния в кристалле. Длина волны , связанная с
электронами, порядка длины волны рентгеновских лучей. Физ смысл волн де
Бройля:квадрат амплитуды волны де Бройля в данной точке пр-ва явл-ся мерой
вероятности обнаружить частицы в этой точке пр-ва.
38 Соотношение неопределенностей
Гейзенберга
 квантовая механика раскрывает
2 основных св-ва вещ-ва: квантованность внутриатомных процессов и волновую
природу частиц. Скорость света в вакууме явл-ся критерием, определяющим границу
применимости классических з-нов, т.к. она явл-ся макс скоростью передачи
сигналов.
квантовая механика раскрывает
2 основных св-ва вещ-ва: квантованность внутриатомных процессов и волновую
природу частиц. Скорость света в вакууме явл-ся критерием, определяющим границу
применимости классических з-нов, т.к. она явл-ся макс скоростью передачи
сигналов.
Т.к.
движущая частица обладает корпускулярно- волновым дуализмом, то одновременное точное
определение координаты х и импульса р невозможно. Чем точнее определена
координата (![]() ) тем менее
точно определен импульс (
) тем менее
точно определен импульс (![]() )
)
Утверждение
о том, что произведение неопределенностей значений двух сопряженных переменных
не может быть по порядку величины меньше постоянной Планка, называется
принципом неопределенности Гейзенберга.
![]()
![]()
![]()
40. Временное и стационарное уравнение Шредингера.
39 Уравнение Шредингера(
![]() . (11)
. (11)
![]() комплексная
функция координат и времени, характеризует состояние микрочастицы. Это основное
уравнение нерелятивистской квантовой механики. Для стационарных состояний оно
имеет вид:
комплексная
функция координат и времени, характеризует состояние микрочастицы. Это основное
уравнение нерелятивистской квантовой механики. Для стационарных состояний оно
имеет вид:
![]() . (12)
. (12)
М. Борн (![]() функции
определяет вероятность dP того, что частица будет обнаружена в пределах объема
dV
функции
определяет вероятность dP того, что частица будет обнаружена в пределах объема
dV
![]() (13)
(13)
А - коэффициент
пропорциональности, для пси-функции выполняется следующее условие нормировки:
![]() (14)
(14)
Из смысла ![]() функции(волновая)
вытекает, что квантовая механика имеет статистический характер. Уравнение
Шредингера позволяет найти пси – функцию данного состояния и, следовательно, определить
вероятность нахождения частицы в различных точках пространства. Из уравнения
(14) и условий, налагаемых на пси – функцию, непосредственно вытекают правила
квантования энергии.
функции(волновая)
вытекает, что квантовая механика имеет статистический характер. Уравнение
Шредингера позволяет найти пси – функцию данного состояния и, следовательно, определить
вероятность нахождения частицы в различных точках пространства. Из уравнения
(14) и условий, налагаемых на пси – функцию, непосредственно вытекают правила
квантования энергии.
Пси – функция должна быть
однозначной, непрерывной и конечной, кроме того она должна иметь непрерывную и
конечную производную – стандартные условия.
41. Частица в одномерной прямоугольной потенциальной яме. Собственные функции. Принцип соответствия.
40 Частица в потенциальной яме
 Пусть частица движется вдоль оси х в бесконечно
глубокой потенциальной
яме ширины l. Потенциальная энергия в этом случае равна нулю внутри
"ямы" и обращается в бесконечность повсюду вне ее (рис. 1).
Пусть частица движется вдоль оси х в бесконечно
глубокой потенциальной
яме ширины l. Потенциальная энергия в этом случае равна нулю внутри
"ямы" и обращается в бесконечность повсюду вне ее (рис. 1).
Из-за бесконечной высоты потенциальных стенок частица не может попасть за пределы
потенциальной ямы, следовательно, вне ямы функция Ψ = 0. Из условия
непрерывности на границах ямы:
![]() . (1)
. (1)
Рис.1
Используем стационарное
уравнение Шредингера:
![]() .
.
В области 0 < x < l
уравнение Шредингера имеет вид:
![]() . (2)
. (2)
Обозначим
![]() . (3)
. (3)
Тогда уравнение примет вид:
Ψ // + k2 Ψ =
0. (4)
Решение:
![]() . (5)
. (5)
Используем (1) для определения
k и α. Из ![]() получим
получим ![]() ,
,
откуда α = 0. Из ![]() имеем
имеем ![]()
![]() и
и
![]() , где n =
1,2,3… (6)
, где n =
1,2,3… (6)
n – главное квантовое число.
Подставим (6) в (3) и найдем
собственные значения энергии:
![]() . (n = 1,2,3…) (7)
. (n = 1,2,3…) (7)
Спектр энергии оказался
дискретным.
Оценим расстояние между соседними
энергетическими уровнями
 .Для молекул (m ~ 10-
.Для молекул (m ~ 10-
Волновая функция имеет вид:
![]() . (8)
. (8)
Используем условие нормировки:
 .
.
На границах функция =0,
поэтому интеграл среднему значению функции, умноженному на длину интервала
ℓ, т.е.
![]() ,
,
откуда ![]() и
и
![]() . (9)
. (9)
Рассмотрим графики.

РИС.2
Принцип соответствия Бора
Рассмотрим влияние квантового
числа n на характер расположения уровней.
Возьмем отношение ![]() . С ростом n
отношение уменьшается, т.е. имеет место относительное сближение уровней.
. С ростом n
отношение уменьшается, т.е. имеет место относительное сближение уровней.
В 1923 году Н. Бор сформулировал принцип
соответствия: При больших квантовых числах результаты и выводы квантовой
механики должны соответствовать классическим выводам и результатам.
42. Прохождение частицы через потенциальный барьер. Туннельный эффект.
41 Прохождение частицы через потенциальный барьер
Рассмотрим 2 случая: классический и
квантовый. (Анимации). В квантовомеханическом случае возможен туннельный
эффект. Вводится коэффициент прозрачности барьера:
 . (10)
. (10)
(10) дает вероятность прохождения волн де
Бройля сквозь потенциальный барьер. По аналогии с оптикой вводится и
коэффициент отражения R=1-D.
Для прямоугольного барьера
![]() . (11)
. (11)
Для произвольного барьера
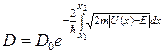 . (12)
. (12)
Туннельный эффект имеет место, когда D не слишком мала, т.е. показатель степени близок к
1. Это возможно при ℓ порядка атомных размеров.
Пример: U-E ≈ 10 eV, me ≈ 10-
Парадокс туннельного эффекта: Если E‹ U, то Екин ‹ 0. Но туннельный эффект чисто
квантовое явление и, кроме того, Е ≠ Ек + Ер из-за соотношения
неопределенностей Гейзенберга.
43. Линейный гармонический осциллятор в квантовой механике. Нулевая энергия.
42 Линейный гармонический осциллятор в квантовой
механике. Нулевая энергия.
Линейный гармонический осциллятор-
система, совершающая одномерное движение под действием квазиупругой силы.
Потенциальная энергия гармонического осциллятора ![]() ,
, ![]() -
собственная частота, m- масса частицы. Зависимость имеет вид параболы, т.е.
«потенциальная яма» в данном случае явл. параболической.
-
собственная частота, m- масса частицы. Зависимость имеет вид параболы, т.е.
«потенциальная яма» в данном случае явл. параболической.
Тогда стационарные состояния
квантового осциллятора опред. у-нием Шредингера![]() , Е- полная
энергия.
, Е- полная
энергия.
![]() - энергия
квантового осциллятора принимает дискретные значения, квантуется. Энергия ограничена снизу отличным от нуля,
как и для прямоугольной «ямы» с бесконечно высокими «стенками», минимальным
значением энергии
- энергия
квантового осциллятора принимает дискретные значения, квантуется. Энергия ограничена снизу отличным от нуля,
как и для прямоугольной «ямы» с бесконечно высокими «стенками», минимальным
значением энергии ![]() .
Существование минимальной энергии – она наз. Энергией нулевых колебаний –
является типичной для квантовых систем и представляет собой прямое следствие
соотношения неопределенностей.
.
Существование минимальной энергии – она наз. Энергией нулевых колебаний –
является типичной для квантовых систем и представляет собой прямое следствие
соотношения неопределенностей.
44. Атом водорода в квантовой теории. Энергетические уровни. Квантовые числа. Спин. Принцип Паули.
43 Атом водорода
1885,
Формула Бальмера: ![]()
R = 2,07.1016 c-1 .
Обобщенная формула
Бальмера: ![]() , (13)
, (13)
где n = m + 1,…
Квантовомеханическая задача: ![]()
![]() .
.
Уравнение Шредингера:
![]() . (14)
. (14)
Решение для стандартных
условий:
![]() . (n = 1,2,3…) (15)
. (n = 1,2,3…) (15)
При n = 1 (основное состояние
атома): Е1 = - 13,6 эВ.
Собственные функции:
![]() . (16)
. (16)
При данном n: ℓ =
0,1,2,…, n-1
При данном ℓ: m = -
ℓ, - ℓ+1, -1, 0, 1,… ℓ-1, ℓ - всего (2 ℓ + 1) значений.
 Энергия зависит
только от n. Следовательно, каждому Еn соответствует несколько собственных
функций
Энергия зависит
только от n. Следовательно, каждому Еn соответствует несколько собственных
функций ![]() с разными
ℓ и m. Разные состояния с одинаковой энергией называются вырожденными.
с разными
ℓ и m. Разные состояния с одинаковой энергией называются вырожденными.
Кратность вырождения
 . (17)
. (17)
Возможные состояния
электронов:
1s
2s 2p
3s 3p 3d
4s 4p 4d
Правило отбора: ![]() . Показать
схему переходов.
. Показать
схему переходов.
В дальнейшем было теоретически
доказано и подтверждено экспериментами существование у электрона (и других элементарных
частиц) собственного момента импульса LS, который не связан с движением
электрона в пространстве. Этот собственный момент был назван спином. Спин
следует считать внутренним свойством, присущим электрону, подобно тому, как ему
присущи заряд или масса.
Модуль собственного момента импульса электрона определяется спиновым квантовым
числом S, равным 1/2 :
![]() , (29)
, (29)
Проекция спина на ось z может
принимать значения
![]() (ms=±s=
±1/2 , (30)
(ms=±s=
±1/2 , (30)
где ms - спиновое квантовое
число.
44 В
классической механике частицы одинаковой природы можно различать. В квантовой
механике в силу принципа неопределенности понятие траектории частицы утрачивает
смысл. Поэтому следить за каждой из одинаковых частиц и тем самым различать их
невозможно. Таким образом, в квантовой механике частицы одинаковой природы
полностью теряют свою "индивидуальность" - они оказываются
неразличимыми.
Принцип неразличимости одинаковых частиц приводит к глубоким физическим
следствиям. Оказывается, что частицы с целым или нулевым спином (бозоны) могут
находиться в пределах данной системы в одинаковом состоянии в неограниченном
количестве. Частицы с полуцелым спином (фермионы) согласно принципу Паули могут
находиться в квантовых состояниях только поодиночке.
Принцип Паули (
Принцип Паули дает объяснение периодической повторяемости свойств атомов в периодической системе элементов Д.И. Менделеева.
45 Спонтанное и вынужденное
излучения. Лазеры.
Атомы
могут нах-ся лишь в квантовых состояниях с дискретными значениями энергии Е1,
Е2,… Ради простоты рассмотрим только два из этих состояний (1 и 2). Если атом
нах-ся в основном состоянии 1, то под действием внешнего излучения может
осуществиться вынужденный переход в возбужденное состояние 2 (рис.1),
приводящий к поглощению излучения. Атом, находясь в возбужденном состоянии 2,
может через нек-ый промежуток времени спонтанно, без каких-либо внешних
воздействий, перейти в состояние с низшей энергией(основное), отдавая
избыточную энергию в виде электромагнитного излучения.(испуская фотон с
энергией ![]() ). Процесс испускания фотона возбужденным атомом
без внешних воздействий наз. Спонтанным излучением. (рис.2) Если на атом,
нах-ся в возбужденном
). Процесс испускания фотона возбужденным атомом
без внешних воздействий наз. Спонтанным излучением. (рис.2) Если на атом,
нах-ся в возбужденном
состоянии
2, действует внешнее излучение, то
возникает вынужденный переход в основное состояние 1 с излучением фотона.(рис
3) При подобном переходе происходит излучение атомов фотона дополнительно к
тому фотону, под действием к-го произошел переход. Возникающее в результате
таких переходов излучение – вынужденное. Т.о., в процесс вынужденного излучения
вовлечены два фотона: первичный фотон, вызывающий испускание излучения
возбужденным атомом, и вторичный фотон, испущенный атомом.
Лазеры
– усиление света с помощью вынужденного излучения. Они генерируют в видимой,
инфракрасной и ближней ультрафиолетовой областях. Идея качественно нового
принципа усиления и генерации электромагнитных волн, примененная в мазерах
(генераторы и усилители, работающие в сантиметровом диапазоне радиоволн) и
лазерах, принадлежит рос. Ученым Басову и Прохорову. Важнейшими из сущ. типов лазеров явл.
твердотельные, газовые, полупроводниковые и жидкостные. Лазер имеет три
основных компонента: 1). Активную среду, в к-ой создаются состояния с инверсией
населенностей, 2). Систему накачки (устройство для создания инверсии в активной
среде), 3). Оптический резонатор (устройство, выделяющее в пространство
избирательное направление пучка фотонов и формирующее выходящий световой
пучок). Свойства лазерного излучения:
1). Временная и пространственная когерентность. Время когерентности составляет
10-3с, что соответствует длине когерентности порядка 105м. 2). Строгая
монохроматичность ![]() 3). Большая
плотность потока энергии. 4). Очень малое угловое расхождение в пучке.
Применяются: для обработки и микросварки твердых металлов, получение и
исследование высокотемпературной плазмы, в измерительной технике, в голографии.
3). Большая
плотность потока энергии. 4). Очень малое угловое расхождение в пучке.
Применяются: для обработки и микросварки твердых металлов, получение и
исследование высокотемпературной плазмы, в измерительной технике, в голографии.
46 В квантовой
статистике системы, состоящие из огромного числа частиц, исследуются с помощью
законов квантовой механики, в основе которых лежат корпускулярно – волновой
дуализм частиц вещества и принцип неразличимости тождественных частиц. Последний
означает, что все одинаковые частицы (например, электроны в металле) являются
неразличимыми друг от друга.
В квантовой статистике ставится задача о
распределении частиц по ячейкам фазового пространства (шестимерного
пространства координат и скоростей), элемент которого равен ![]() , а также
задача определения средних значений физических величин, характеризующих макроскопическое
состояние системы. Состоянию частицы в фазовом пространстве, с учетом
соотношения неопределенностей Гейзенберга, соответствует не точка, а ячейка
фазового объема h3, где h – постоянная Планка.
, а также
задача определения средних значений физических величин, характеризующих макроскопическое
состояние системы. Состоянию частицы в фазовом пространстве, с учетом
соотношения неопределенностей Гейзенберга, соответствует не точка, а ячейка
фазового объема h3, где h – постоянная Планка.
Частицы, число которых равно ΔNi в объеме ΔГi , могут различными способами
распределиться между Δgi
состояниями с энергией Ei. Тогда число
квантовых состояний в объеме ΔГi с энергиями от Ei до Ei + ΔEi равно
![]() . (1)
. (1)
Среднее значение любой функции
определяется с помощью функции распределения, которая позволяет также найти
вероятность данного состояния системы.
Ф-ция распред-ия Ф-Д. фазовое пр-во – пр-во 6
измерений, где состояние каждой частицы опредл-ся 6 координатами.
В квантовой механике различают два вида
частиц: бозоны – частицы с целым
или нулевым спином (в единицах![]() ), на
которые не распространяется принцип Паули и подчиняющиеся распределению
Бозе-Эйнштейна (например, некоторые
ядра, фотоны, фононы) и фермионы –
частицы с полуцелым спином (электроны, протоны, нейтроны и т.д.). Последние
описываются квантовой статистикой Ферми-Дирака и подчиняются принципу Паули, согласно которому в каждом
квантовом состоянии может находиться только одна частица. Функция распределения Бозе-Эйнштейна fБ
выражает среднюю “населенность” бозонами состояний с данной энергией или
среднее их число в одном состоянии:
), на
которые не распространяется принцип Паули и подчиняющиеся распределению
Бозе-Эйнштейна (например, некоторые
ядра, фотоны, фононы) и фермионы –
частицы с полуцелым спином (электроны, протоны, нейтроны и т.д.). Последние
описываются квантовой статистикой Ферми-Дирака и подчиняются принципу Паули, согласно которому в каждом
квантовом состоянии может находиться только одна частица. Функция распределения Бозе-Эйнштейна fБ
выражает среднюю “населенность” бозонами состояний с данной энергией или
среднее их число в одном состоянии:
![]() ,
,
где ![]() - число частиц
с энергией в интервале от Ei до Ei + ΔEi;
- число частиц
с энергией в интервале от Ei до Ei + ΔEi;
![]() - число квантовых состояний в этом
интервале энергий.
- число квантовых состояний в этом
интервале энергий.
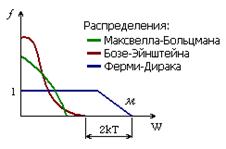 Распределение бозонов по энергиям получается из канонического распределения
Гиббса при условии сохранения энергии E в системе и числа частиц N:
Распределение бозонов по энергиям получается из канонического распределения
Гиббса при условии сохранения энергии E в системе и числа частиц N:
 (2)
(2)
где k – постоянная Больцмана,
Т – термодинамическая температура,
μ – химический потенциал,
равный работе, совершаемой в изобарно-изотермических условиях при увеличении
числа частиц в системе на единицу.
m ≤ 0, иначе среднее
число бозонов в данном состоянии становится отрицательным, что лишено смысла.
Функция распределения Ферми-Дирака
определяется аналогично:
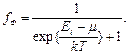 (3)
(3)
Здесь μ, в отличие от
(13.2), может быть положительным.
Функции распределения в классической
(Максвелла-Больцмана) и квантовой статистиках, интерпретируемые как среднее
число частиц в одном состоянии, можно выразить единой формулой:
![]() (4)
(4)
Для распределения Максвелла-Больцмана
δ = 0 и μ = 0, для распределения Бозе-Эйнштейна δ = -1 и для
распределения Ферми-Дирака δ = +1. Все три распределения показаны на рис.
1.
Система частиц называется вырожденной,
если ее свойства описываются квантовыми закономерностями. Вырождение становится
существенным для бозе- или ферми-газов при низких температурах и больших
плотностях.
Рис. 1
Параметром вырождения А называется величина ![]() При A<<1 (малое вырождение) в (13.4)
можно пренебречь величиной δ и квантовые функции распределения переходят
в классическую. Параметр А определяется из условия сохранения общего числа
частиц:
При A<<1 (малое вырождение) в (13.4)
можно пренебречь величиной δ и квантовые функции распределения переходят
в классическую. Параметр А определяется из условия сохранения общего числа
частиц:
![]() (5)
(5)
где n – концентрация частиц, m
– масса частицы, Т – температура, k –постоянная Больцмана, h – постоянная
Планка.
Примером вырожденного газа
являются электроны в металле, которые не подчиняются классической статистике
Максвелла-Больцмана.
47 Согласно корп-волн. дуализму свойств ве-ва, упругим волнам в кристалле
сопоставляют фононы, обладающ. энергией ![]() . Фонон есть квант энергии звук. волны.
Фононы явл. квазичастицами – элемент.
возбуждениями, ведущими себя подобно микрочастицам. Квазичаст. существ. только
в кристаллах. Свойства импульса фонона: при столк. фононов в крист. их импульс
может дискретн. порциями передав. крист.
решетке – он при этом сохраняется. Поэтому в случ. фононов говорят о
квазиимпульсе.
. Фонон есть квант энергии звук. волны.
Фононы явл. квазичастицами – элемент.
возбуждениями, ведущими себя подобно микрочастицам. Квазичаст. существ. только
в кристаллах. Свойства импульса фонона: при столк. фононов в крист. их импульс
может дискретн. порциями передав. крист.
решетке – он при этом сохраняется. Поэтому в случ. фононов говорят о
квазиимпульсе.
Класс.
теория не смогла объяснить завис. теплоемкости
тв. тел от температуры, а квант. статист. решила эту задачу, колеб
атомов в крист решетке не явл независимыми.
48
49
50 Энергетические зоны в
кристаллах. Металлы, диэлектрики и полупроводники в зонной теории твердых тел.
Образ
зонного энерг спектра в крист явл
квант-мех эффектом и вытекает из соотн неопред. В крис валентные
электроны атомов, связ слабее с ядрами, чем внутр электр, могут перех от атома
к атому сквозь потенц барьеры. Энерг внеш эл может принимать значения в
пределах разрешенных энергетических зон.
Разрешенные энергетические зоны разд зонами запрещ значений, наз запр
энерг зонами.
Различия
в электрических свойстах твердых тел объясняются в зонной теории различным
заполнением электронами разрешенных энергетических зон. Эти два фактора
определяют отнесение данного твердого тела к проводникам электрического тока
или к диэлектрикам. Необходимым условием возможности для того, чтобы твердое
тело могло быть проводником, является наличие свободных энергетических уровней,
на к-рые электрическое поле могло бы перевести электроны. Следует учитывать,
что это поле может вызвать лишь внутризонные переходы электронов. Если зона не
полностью занята валентными электронами,
то твердое тело всегда является проводником электрического тока.
Полупроводниками называются твердые тела, у которых валентная зона отдалена от
пустой зоны проводимости ( при Т=0 К) сравнительно узким интервалом энергии dW,
меньшим, чем у диэлектрических кристаллов. У кремния dW = 1,1 эВ
51 Элементы квантовой теории
проводимости металла. Явл-ие сверхпроводимости
квантовая
теория электропроводности металла – теория электропроводности, основывающаяся
на квантовой механике и квантовой статистике Ф-Д. Удельная электрич
проводимость металла ![]() , где lF – средняя длина свободного
пробега электрона, имеющего энергию Ферми, UF- средняя скорость теплового
движения электрона.
, где lF – средняя длина свободного
пробега электрона, имеющего энергию Ферми, UF- средняя скорость теплового
движения электрона.
Состояние
проводника, при к-ом его сопротивление равно нулю, наз сверхпроводимостью.
Сверхпрводящее состоянию соотв-ет полному перекрыванию зон, т.е. зона уровней
электропроводимости в металлах полностью перекрывается с валентной зоной, т.к. ![]()
52 Полупроводники
 Полупроводниками (рис. 6) являются вещества, удельное сопротивление
которых изменяется в широком интервале от 10-5 до 108 Ом.м и очень быстро
уменьшается с ростом температуры. Наиболее широко применяются такие
полупроводники, как Si и Ge. Различают
собственные и примесные полупроводники.
Полупроводниками (рис. 6) являются вещества, удельное сопротивление
которых изменяется в широком интервале от 10-5 до 108 Ом.м и очень быстро
уменьшается с ростом температуры. Наиболее широко применяются такие
полупроводники, как Si и Ge. Различают
собственные и примесные полупроводники.
Собственными являются
химически чистые полупроводники. В них при Т = 0 К все уровни валентной зоны
(ВЗ) заполнены электронами и в зоне проводимости электроны отсутствуют (рис.
15.3). Электрическое поле не может перебросить их из валентной в зону
проводимости (ЗП), поэтому собственные полупроводники при Т = 0К ведет себя как
диэлектрики. При Т > 0 К в результате тепловой генерации часть электронов
переходит с верхних уровней ВЗ на нижние уровни ЗП. Вследствие образования
вакантных уровней в ВЗ поведение электронов ВЗ может быть представлено как
движение положительно заряженных квазичастиц, называемых дырками.
Распределение электронов по
уровням ВЗ и ЗП подчиняется распределению Ферми-Дирака (рис. 7).
У собственных полупроводников значение уровня
Ферми равно
 . (15)
. (15)
Рис.7
где ΔЕ – ширина
запрещенной зоны; mД* и mЭ* - эффективные массы
дырки и электрона в ЗП. Обычно второе слагаемое мало и EF = ΔE/2.
Электропроводность собственных полупроводников
зависит от температуры по следующему закону
![]() (16)
(16)
где ΔЕ – ширина ЗЗ,
σ0 – константа.
Имея температурную зависимость lnσ от 1/T,
можно по графику определить ширину
запрещенной зоны полупроводника ΔЕ.
Примесная
проводимость делится на электронную (или n-типа) и дырочную (р-типа)
проводимость. Для получения полупроводника n-типа (например, кремния (Si) –
элемента IY группы) вводят донорную примесь, т.е. элемент Y группы (фосфор,
мышьяк и т.д.). Атом Si имеет по своему
строению 4 соседних атома, с которыми, отдавая по одному электрону, образует
ковалентные связи. Пятый электрон ато ма примеси остается “лишним”. Энергетические уровни
таких электронов располагаются ниже дна ЗП, для перевода электронов в которую
требуется небольшая энергия (для As в Si ΔEД = 0,054 эВ), получаемая,
например, при тепловом возбуждении. При замещении атома Si трехвалентным атомом
акцепторной примеси (бор, алюминий и т.д.) возникает недостаток одного
электрона для образования насыщенных ковалентных (атомных) связей. Недостающий
электрон может быть позаимствован у соседнего атома Si, у которого появляется
при этом положительная дырка. Последовательное заполнение дырок соседними
электронами эквивалентно движению дырок и приводит к проводимости
полупроводника. Акцепторные уровни возникают в ЗЗ полупроводника выше потолка
ВЗ (для В в Si ΔEА = 0,08 эВ), переход электронов из ВЗ на акцепторные
уровни приводит к появлению в ВЗ дырок. Обратный переход соответствует разрыву
одной из четырех ковалентных связей атома примеси с соседями и рекомбинации
образовавшегося при этом электрона и дырки. (Можно рис. Из Детлафа).
ма примеси остается “лишним”. Энергетические уровни
таких электронов располагаются ниже дна ЗП, для перевода электронов в которую
требуется небольшая энергия (для As в Si ΔEД = 0,054 эВ), получаемая,
например, при тепловом возбуждении. При замещении атома Si трехвалентным атомом
акцепторной примеси (бор, алюминий и т.д.) возникает недостаток одного
электрона для образования насыщенных ковалентных (атомных) связей. Недостающий
электрон может быть позаимствован у соседнего атома Si, у которого появляется
при этом положительная дырка. Последовательное заполнение дырок соседними
электронами эквивалентно движению дырок и приводит к проводимости
полупроводника. Акцепторные уровни возникают в ЗЗ полупроводника выше потолка
ВЗ (для В в Si ΔEА = 0,08 эВ), переход электронов из ВЗ на акцепторные
уровни приводит к появлению в ВЗ дырок. Обратный переход соответствует разрыву
одной из четырех ковалентных связей атома примеси с соседями и рекомбинации
образовавшегося при этом электрона и дырки. (Можно рис. Из Детлафа).
При повышении температуры концентрация
примесных носителей быстро достигает насыщения, т.е. примесная проводимость
доминирует при низких Т, с ростом температуры увеличивается вклад собственной
проводимости. Таким образом, проводимость полупроводника при высоких Т
становится смешанной.
53 Контакт эл и дыр полупров.
Полупров диод.
Полупров
устройссво, содерж один р-n переход, наз
полупров диодом. Они дел на точечные и плоскостные. Благодаря малой емкости
контактн слоя точечные диоды примен в кач детекторов (выпрямителей) высокочаст
колеб вплоть до сантиметр диапазона длин
волн.
Полупроводники n-типа. Если в кристаллическую
решётку четырехвалентного полупроводника, например кремния, внедрить
пятивалентный атом, например фосфор, то для образования ковалентных связей с
соседями ему надо четыре электрона. Пятый же электрон вследствие теплового
движения может оторваться от атома. в результате этого атомы примеси превращаются
в положительные ионы. И появляются
свободные электроны, обусловливающие проводимость полулроводника. Такие
примеси называются донорными, а сам полупроводник называют полупроводник
n-типа (от слова negative — отрицательный).
б) Полупроводники р-типа. Если внедрить
в кристаллическую решетку четырёхвалентного полупроводника (кремния)
трёхвалентный атом (бор), то для образования ковалентной связи с соседями ему
надо четыре электрона, а у него их только три. Поэтому одна связь оказывается
не укомплектованной. Атом бора захватывает один электрон от соседнего атома
кремния, так как это энергетически выгодно. В результате этого атомы примеси
превращаются в отрицательные ноны, а в полупроводнике возникают дырки,
обусловливающие его электропроводность. Проводимость этого типа называется
дырочной, примесь — акцепторной, а полупроводник - р-типа (от слова positive — положительный).
54 Вырожденный эл газ в металле.
Уровень Ферми.
Система
частиц наз вырожденной, если ее св-ва существенным образом отличаются от св-в
системы, подчиняющихся классической статистике. Газ, к-ый подчинятеся квантовой
статистике – вырожденный. Основным признаком вырождения газа явл-ся
независимость энергии его частиц от температуры. Эл газ в металле остается
вырожденным до тех пор, пока любой из электронов не сможет обмениваться
энергией с кристаллической решеткой. Это возможно лишь в том случае, когда ср
энергия тепловых колебаний решетки кТ не меньше энергии Ферми ![]() .
Температура Ферми:
.
Температура Ферми: ![]() - х-ет
переход газа из невырожденного состояния в вырожденное.
- х-ет
переход газа из невырожденного состояния в вырожденное.
Температура
вырождения ![]() . Эл газ в
металле:
. Эл газ в
металле: ![]()
![]()
![]()
![]() - квантовая, подчиняется распределению Ф-Д
- квантовая, подчиняется распределению Ф-Д
Наив
энергетич уровень, занятый электронами, наз уровнем Ферми.
![]() - макс
кинетич энергия, к-ую могут иметь электроны в металле при Т=0К – энергия Ферми
- макс
кинетич энергия, к-ую могут иметь электроны в металле при Т=0К – энергия Ферми 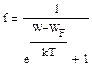 уровень ферми тем выше, чем больше плотность
электронного газа
уровень ферми тем выше, чем больше плотность
электронного газа
55 Атомное ядро и его
характеристики. Состав и строение атомного ядра. Изотопы.
Атом
сост из полож заряж ядра и имеет размеры прим - ![]() м. атомное
ядро сост из элем част – протонов и нейтронов. Протон-полож заря, равный зар
электрона, и массу покоя
м. атомное
ядро сост из элем част – протонов и нейтронов. Протон-полож заря, равный зар
электрона, и массу покоя ![]() кг. Нейтрон- нейтр частица. Протоны и нейтр
наз нуклонами. Общее число нуклонов в ядре наз массовым числом А. атомное ядро
характ зарядом
кг. Нейтрон- нейтр частица. Протоны и нейтр
наз нуклонами. Общее число нуклонов в ядре наз массовым числом А. атомное ядро
характ зарядом ![]() ,число
протонов в ядре.
,число
протонов в ядре.
56 Дефект массы и энергия связи ядра.
Деф
масс- разность м/у суммарной массой протонов и нейтронов, измеряемых в
свободном состоянии, и массой ядра
Масса
ядра меньше, чем сумма масс составляющих его нуклонов. Энергия которую
необх затратить, чтобы расщепить ядро на
отдельные нуклоны, наз энергией связи ядра. ![]()
57
58 Ядерные силы и
их основные свойства.
Между
составляющ ядро нуклонами действ особые силы, знач превыш кулоновские силы
отталкив между протонами, наз ядерными силами.
Свойства: яд силы явл силами притяжения, яд силы явл короткодействующие-
их действие проявл только на расст прим ![]() м, заряд
независимость, насыщение, взаимная ориентация спинов.
м, заряд
независимость, насыщение, взаимная ориентация спинов.
59 Самопроизв излучение наз радиоакт распадом. Способность некотор аьомных
ядер самопроизв превращ в др ядрас испуск различ видов радиоакт излучений.
Радиоакт разд на естественную и искусственную. Рад изл быв трех видов - ![]() .
.
![]() -закон
радиоакт распада.
-закон
радиоакт распада.
Альфа-распадом
наз. самопроизв. распад ядра (X) на альфа-частицу (ядро атома гелия 2He4) и
ядро продукт (Y) по след. схеме” ZXA=2He4+Z-2YA-4, a-лучи
обл. наим. проник. способн.
Бета-распад-явление
эл. b-распада предст. собой превр. атомн. ядра (Х)
путем испуск. эл. (е) по схеме: ZXA=-1e0+Z+1YA, проник. спос. b-част.
(эл.)выше, чем а-частиц.
Гамма-лучи-это
жесткое электромагн. излуч оч. выс. частоты. Из-за выс. частоты у g-лучей
сильно выраж. квант. св-ва, и они ведут себя как поток частиц-g-квантов:
g-лучи обл. наиб. проник. способн.
60 Радиоактивный распад ядер.
Закономерности и происхождение альфа-,
бета-, гамма-излучений.
![]() -изл отклон
элетр и магн полями, предст собой поток ядер гелия,заря +2е, а масса совпадает
с массой изотопа гелия(2,4).
-изл отклон
элетр и магн полями, предст собой поток ядер гелия,заря +2е, а масса совпадает
с массой изотопа гелия(2,4).![]() -изл откл
Эл и магн полями, его иониз способность знач меньше(на 2 порядка ), а проникающ
способность значительно больше. Предст собой поток быстр электронов. Сильно
рассеив в ве-ве.
-изл откл
Эл и магн полями, его иониз способность знач меньше(на 2 порядка ), а проникающ
способность значительно больше. Предст собой поток быстр электронов. Сильно
рассеив в ве-ве.
![]() -изл не откл
Эл и магн полями, слабая иониз способность, большая проникающая
способность. При прохожд через крист
обнаруж дифракцию. Ярко выраженные корпускулярные свойсвта.
-изл не откл
Эл и магн полями, слабая иониз способность, большая проникающая
способность. При прохожд через крист
обнаруж дифракцию. Ярко выраженные корпускулярные свойсвта.
61 яд реакции и законы сохр.
Яд
реакции-это превращ атомных ядер при взаимодействии с элемент частицами или
друг с другом. X+a-Y+b, или X(a,b)Y, эффективность взаимодейств хар-ют
эффективным сечением ![]() .
. ![]() =dN/nNdx.
Ед [барн]. В любой яд реакции вып-ся законы сохр Эл зарядов: сумма зарядов,
вступ в яд реакцию равна сумме зарядов конечных прод реакции. Вып-ся также
законы сохр энергии, импульса и мом импульса.
=dN/nNdx.
Ед [барн]. В любой яд реакции вып-ся законы сохр Эл зарядов: сумма зарядов,
вступ в яд реакцию равна сумме зарядов конечных прод реакции. Вып-ся также
законы сохр энергии, импульса и мом импульса.
термоядерные реакции:
при
T@10^8 К, за счет теплового движения частиц ядра
могут соударяться, а электроны “падать” на ядра (Fкинетическая >
Fкулона)и может происходить синтез новых ядер при этом выделяется огромная
энергия 0,82 Мэв/нуклон