Лекция 8

Тема  8. Активные фильтры

8.1 Классификация фильтров

 

      Электрический фильтр – это устройство для усиления или ослабления отдельных частот или полосы частот, проходящих через это устройство.

     Активный фильтр в отличие от пассивного содержит, кроме резисторов и конденсаторов, операционный усилитель.

     Фильтры классифицируются:

А. По пропускаемым (или подавляемым) частотам на:

1) фильтр низких частот (рис.8.1,а);

Рисунок 8.1 – АЧХ фильтров: а – НЧ; б - ВЧ

где  f = 0 ÷ fср – полоса пропускания;  f > fср - полоса подавления заграждения;

f_ср÷ f_nд ‑ переходной участок; f_nд – частота, при которой коэффициент усиления K на 3дБ больше, чем в полосе подавления.

2) фильтр высоких частот (рис.8.1,б);

- полоса пропускания f_проп = от f_ср до ∞;

- полоса затухания f_затух = от 0 до f_nд;

- от f_nд до f_ср – переходной участок;

3) полосовой фильтр (рис.8.2,а);

    

Рисунок 8.2 – АЧХ полосового (а) и режекторного (б) фильтров

где f_в – f_н – полоса пропускания;

f₀ – средняя центральная частота

4) режекторный или заградительный фильтр (рис.8.2,б)

- полоса пропускания П_проп = 0 ÷ f_н и П_проп = f_в ÷ ∞;

- полоса подавления f_nд = f_н ÷ f_в.

     Если  полоса подавления узкая f_nд, то такой фильтр  называется фильтр-пробкой. Используется для подавления нежелательных частот, например, 50 Гц в звуковой аппаратуре.

     Достоинства активных фильтров:

­        используются только конденсаторы и резисторы (их свойства ближе к идеальным, чем у индуктивностей);

- относительно дешевые;

- усиление отфильтрованного сигнала;

- возможность увеличения каскадов фильтра для улучшения АЧХ;

- малогабаритность.

     Недостатки:

- наличие источника питания;

- рабочий диапазон частот ограничен максимальной рабочей частотой ОУ. (не более несколько мГц).

Б. По наклону переходного участка АЧХ:

Рисунок 8.3 – АЧХ фильтров: а – Баттерворта; б – Чебышева;

в - Бесселя

1) фильтр Баттерворта (рис.8.3,а);

АЧХ фильтра в полосе пропускании ∆f  равномерна и  максимально плоская.

АЧХ фильтра первого порядка имеет наклон характеристики 20дБ/декаду, а АЧХ фильтра 5-го порядка 100 дБ/декаду.

     Время, за которое сигнал проходит через фильтр, от частоты зависит нелинейно. Поэтому ступенчатый сигнал на входе фильтра Баттерворта вызывает выброс на выходе фильтра. Используется в случаях, когда надо иметь одинаковые коэффициенты усиления К для всех частот в полосе пропускания;

2) фильтр Чебышева (рис.8.3,б);

АЧХ фильтра имеет волнообразные зубцы в полосе пропускания и равномерна в полосе подавления. Амплитуда зубцов (U_m) может достигать 0.5; 1; 2; 3 дБ.

При увеличении порядка фильтра наклон переходного участка круче, но неравномерна полоса пропускания. Фильтр Чебышева используется в устройствах, где нужен очень крутой наклон характеристики.

3) фильтр Бесселя (рис.8.3,в);

 Это фильтр с линейной задержкой. Время прохождения сигнала через фильтр линейно зависит от частоты. Используется для фильтрации импульсных сигналов, которые меньше искажаются, чем при прохождении через фильтр Баттерворта.

     Фильтры характеризуются следующими параметрами:

а) порядок фильтра  (число его полюсов);

     Один полюс обусловлен одной RC-цепью. Например, фильтр НЧ второго порядка – это двухполюсный фильтр, имеет наклон 40дБ/декаду.

     Три последовательно соединенных фильтра второго порядка составляют один фильтр – шестого порядка. Наклон характеристики на переходном участке равен 120дБ/дек.

б) коэффициент затухания a;

     Определяет тип фильтра и форму АЧХ в полосе пропускания и вблизи переходного участка.

     Таким образом, одна и та же схема, в зависимости от выбора значений коэффициента затухания a, может быть фильтром Баттерворта, Чебышева или Бесселя (рис.8.4).

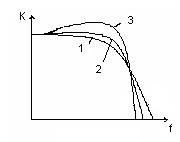
Рисунок 8.4 – АЧХ различных фильтров: 1 – фильтр Бесселя при a = 1,732;

2 - фильтр Баттерворта при a = 1,414; 3 - фильтр Чебышева при a = 1,059

в) добротность Q связывает среднюю частоту  и ширину полосы пропускания f_проп на уровне 3дБ

     Добротность   ‑ обратно пропорциональна коэффициенту затухания.

8.2 Схемы активных фильтров

8.2.1 Фильтры Саллена-Ки

 

     С ростом порядка фильтра фильтрующие свойства улучшаются. На одном ОУ достаточно просто реализуется фильтр второго порядка. Для реализации фильтров нижних, верхних и полосовых частот широкое применение нашла схема фильтра второго порядка Саллена-Ки (рис.8.5).

Рисунок 8.5 - Схема активного ФНЧ второго порядка Саллена-Ки

     ООС, сформированная с помощью делителя напряжения R₃, R₄ = R₃(K – 1), обеспечивает коэффициент усиления, равный К.

 – интегрирующие цепи.

     Поменяв местами сопротивления и конденсаторы в схеме (рис.8.5) получим фильтр верхних частот  ФВЧ(8.6).

Рисунок 8.6 – Схема активного ФВЧ второго порядка Саллена-Ки

где  – дифференцирующие цепи.

    Имеются две RC-цепи, следовательно, это фильтр второго порядка.

     Коэффициент передачи                                   

                                                                                    (8.1)

     Сопротивления R₃ и R₄ - определяют коэффициент затухания и тип фильтра.

     Характеристика вблизи края П_проп формируется за счет ОС, которая осуществляется за счет С₁  в ФНЧ, C₂ ‑ в ФВЧ.

     Полосовой фильтр второго порядка можно реализовать на основе схемы Саллена-Ки  (рис.8.7).

Рисунок 8.7 – Схема активного полосового фильтра Саллена-Ки

.     Параметры фильтра рассчитываются по формулам

                                                 (8.2)

где f_p – резонансная частота; α – коэффициент передачи ООС через ДН.

     Достоинство схемы – ее добротность зависит от параметра α, тогда как резонансная частота от этого параметра не зависит.

 

8.3 Расчет параметров схемы активного ФВЧ Чебышева

 

     На (рис.8.8) приведена схема активного фильтра высокой частоты (ФВЧ) 2-го порядка Чебышева.

Рисунок 8.8 – Схема активного ФВЧ 2-го порядка Чебышева

Любой полиноминальный фильтр порядка n (т.е. такой, что его передаточная функция представляет собой отношение полиномов) может быть представлена последовательным соединением фильтров 2-го порядка.

     Тогда передаточная функция (ПФ) активного ВЧ фильтра n-го порядка примет вид

           (8.3)

где m – количество звеньев 2-го порядка; К – коэффициент усиления фильтра n-го порядка; a_i , b_i – коэффициенты полиномов ПФ фильтра, берутся из (табл. 8.1).

     Формула (8.3) ПФ фильтра получается из законов теории автоматического управления, т.е равна отношению изображений выходного напряжения к входному:

               (8.4)

     Расчетным путем установлено, что для достижения приемлемого ослабления колебаний в области частот пропускания (A_{P MIN} = 0,5 дБ) коэффициенты ПФ фильтра a_i , b_i    должны иметь строго определенные значения. (табл.8.1).

Таблица 8.1 – Коэффициенты полиномов ПФ для фильтров 2, 4 и 6 порядков

Фильтр Чебышева, AP MIN = 0,5 дБ	Порядок фильтра n
	2	4		6
	Номер и количество звеньев m
	1	1	2	1	2	3
a	1,3614	2,6282	0,3648	3,8645	0,7528	0,1589
b	1,3827	3,4341	1,1509	6,9797	1,8573	1,0711

    

     Если коэффициенты ПФ фильтра a_i , b_i  известны и для простоты расчета положить, что С₁ = С₂ = С, то, используя (8.3 и 8.4) и приравняв коэффициенты двух ПФ, определим сопротивления схемы

                                                               (8.5)

где ω_С – круговая частота среза, которая определяется через граничную частоту пропускания f_п и равна

ω_С = 2π f_п .

     Эмпирическим путем установлено, что для приемлемых величин сопротивлений и постоянных времени фильтра, емкость С выбирается близким отношению

                                                                                                (8.6)

где f_З – граничная частота задержки.

     Отрицательная обратная связь ОУ, образованная делителем напряжения R₃, R₄ = (K – 1)R₃, обеспечивает коэффициент усиления равным К. R₃ можно принять равным 1кОм, тогда по известному К определяется второе сопротивление.

     Таким образом, по формулам (8.5 и 8.6) и R₃ = 1кОм определены электрические параметры схемы активного ФВЧ Чебышева.