Тема 4. Линейные схемы на основе ОУ

4.1 Усилители сигналов на ОУ

4.1.1 Инвертирующий масштабный усилитель

 

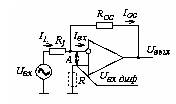
Рисунок 4.1 – Схема инвертирующего масштабного ОУ

     Допустим, что                     К_дф → ∞ и R_вх → ∞ .                                (4.1)

     Следовательно, U_вхдф → 0. Тогда т.А можно считать закороченной на землю.

По первому закону Кирхгофа I₁ = I_вх + I_ос, а т.к. R_вх → ∞, то I_вх = 0 и I₁ = I_ос.

Коэффициент усиления инвертирующего масштабного усилителя равен

                                                           (4.2)

     Из (4.2) видно, что K_U коэффициент усиления  по напряжению инвертирующего масштабного усилителя не зависит от параметров ОУ, а определяется только видом обратной связи.  Здесь имеет место параллельная ООС по напряжению.

     При R_ос = R₁ → K_U = -1, усилитель (рис.4.1) является инвертором.

     Для симметрирования (уравнивания) входных токов ставится резистор R, который определяется как параллельно соединенные R_ос и R₁

4.1.2 Неинвертирующий масштабный усилитель

 

     На (рис.4.2,а) представлена схема неинвертирующего масштабного  усилителя. Цепь R_ос – R₁ создает последовательную ООС по напряжению. Входной сигнал подается на неинвертирующий вход. Согласно (4.1) I₁ = I_oc .

Из (рис.4.2,а)  находим

U_вх = I₁R₁,  U_вых = I₁ (R₁+R_ос).

    Коэффициент усиления неинвертирующего масштабного усилителя равен

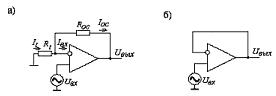
Рисунок 4.2 – Схема инвертирующего масштабного ОУ (а) и повторитель напряжения (б)

     Если R_oc = 0 и R₁ = ∞, K_U = 1 (рис.4.4,б), то это повторитель напряжения. Имеет место 100% последовательная ООС по напряжению. Сигнал на выходе повторяет входной сигнал.

4.2 Решающие усилители на ОУ

4.2.1 Инвертирующий сумматор

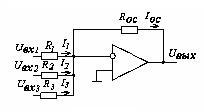
Рисунок 4.3 – Схема инвертирующего сумматора

     Из (рис.4.3) следует, что I_ос = I₁ + I₂ + I₃, т.к. R_вх→ ∞, I_вх = 0,

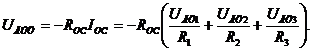
     Если R₁ = R₂ = R₃ = R, то

4.2.2 Вычитающий усилитель

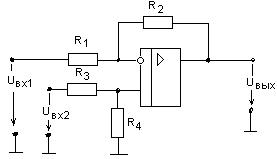
Рисунок 4.4 – Вычитающий усилитель

При U_вх2 = 0     - выход инвертирующего усилителя.

При U_вх1 = 0   - вход неинвертирующего усилителя.

 - выход неинвертирующего усилителя.

     В соответствии с принципом суперпозиции

     При R₁ = R₂ = R₃ = R₄                     U_вых = U_вх2 – U_вх1.

 

4.2.3 Инвертирующий интегратор

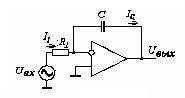
Рисунок 4.5 – Схема инвертирующего интегратора

     Из условия (4.1) следует, что U_вых = - U_c. Ток через конденсатор C равен

а входной ток I₁ = U_вх/R₁. По условию (4.1),  I_вх = 0 и I₁ = I_c.

Следовательно,

Отсюда, проинтегрировав, получим 

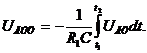
     U_вых линейно зависит от U_вх, т.е. схема интегратора является простейшей схемой генератора линейно изменяющегося напряжения (ГЛИН).

     В операторной форме ПФ интегратора равна

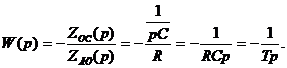
4.2.4 Инвертирующий суммирующий интегратор

 

     Если I_вх = 0 из-за R_вх = ∞, то

 или

     При R₁ = R₂ = R₃ = R

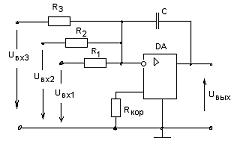
Рисунок 4.6 – Схема трехвходового инвертирующего суммирующего интегратора

4.2.5 Инвертирующий дифференциатор

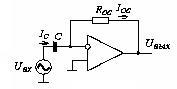
Рисунок 4.7 – Схема инвертирующего дифференциатора

     Ток через R_ос  равен ,  а ток через емкость С 

     Так как I_вх = 0, то I_oc = I_c и 

     Отсюда                                 

     В операторной форме ПФ дифференциатора равна

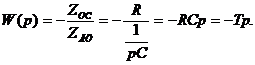
4.2.6 Инвертирующий логарифмирующий преобразователь

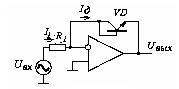
Рисунок 4.8 – Схема инвертирующего логарифмирующего преобразователя

     Очевидно, что  I_д = I₁,                 

где ,  , φ_Т – температурный потенциал p-n перехода; I_o – тепловой ток. Для кремневого диода I_o = 1нА, φ_Т = 25мВ при комнатной температуре.

     Следовательно,

.

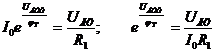      Прологарифмировав, получим               

.

4.2.7 Аналоговые перемножители

 

     По принципу действия схемы перемножителей можно разделить на следующие группы:

- перемножители на основе управляемого источника тока;

- перемножители с управляемым сопротивлением канала полевого транзистора;

- логарифмирующие-антилогарифмирующие перемножители;

- импульсные перемножители;

- перемножители на основе ЦАП.

 

Перемножители на основе управляемых источников тока

 

     Упрощенная схема перемножителя, реализующего этот метод представлен на (рис.4.9). Операция умножения реализуется за счет изменения коэффициента передачи дифференциального усилительного каскада (согласованные транзисторы VT₁ и VТ₂) при изменении его рабочего тока I₁. В данном случае I₁ = U_y/R₁, благодаря применению токового зеркала (согласованные транзисторы VT₃ и VT₄) и источника тока на транзисторе VT₅.

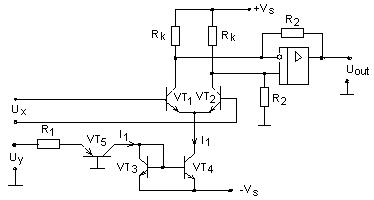
Рисунок 4.9 – Схема перемножителя на основе управляемого

источника тока

     Вычитатель формирует напряжение, прямо пропорциональное разности коллекторных токов  VT₁ и VT₂:

U_out = R₂(I_k2 – I_k1),

причем разность коллекторных токов определяется отношением входного на­пряжения дифференциального каскада к динамическому сопротивлению эмит­тера r_E транзисторов VT₁ и VT₂:

I_k2 – I_k1 = U_x/r_E.

     В свою очередь, динамическое сопротивление эмиттера обратно пропорцио-нально току I₁:

     Тогда                                             

     Отсюда следует, что

     Приведенная схема имеет ограниченное практическое применение из-за свойственных ей серьезных недостатков. Во-первых, для того, чтобы искаже­ния не превышали 1% необходимо соблюдать условие |U_x| < 9 мВ. Во-вторых, коэффициент передачи перемножителя зависит от температуры. В-третьих, для того, чтобы схема работала правильно, напряжение U_y должно быть только по-ложительным, в то время как U_x может иметь любой знак. Такой перемножи­ть называется двухквадрантным. Выпускаемые промышленностью четырех-квадрантные перемножители на основе управляемых источников тока имеют значительно более сложную внутреннюю структуру. Примерами могут служить: классический AD534 фирмы Analog Devices, имеющий погрешность перемножения не более 0 1 % в диапазоне входных сигналов ±10 В и частотном диапазоне до 10 МГц. Связь между входными и выходными сигналами этих микросхем устанавливается соотношением:

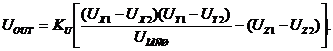
     Микросхемы можно использовать как умножитель или как делитель (рис.4.10).

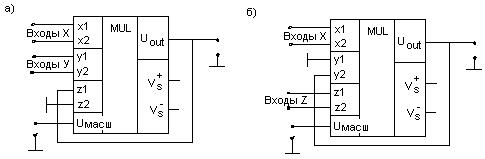
Рисунок 4.10 – Схемы включения перемножителей:

а – аналоговый умножитель; б – аналоговый делитель

     При включении микросхемы умножителем (рис.4.10,а) можно записать:

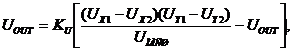
или

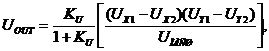
     При K_U >> 1:

.

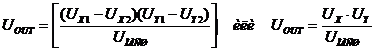     При включении делителем (рис.4.10,б) можно записать:

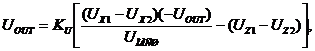
 при K_U >> 1:

.

     Аналоговые перемножители могут использоваться и для выполнения иных математических операций над сигналами, таких как возведение в квадрат, извлечение квадратного корня и др.

     Схемы квадратора и извлечения квадратного корня получаются путем соединения обратной связи в ИМС AD534.

     Если соединить входы х₁ , у₁ и заземлить входы x₂, y₂ и z₂, то получим схему квадратора

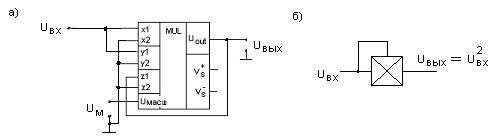
Рисунок 4.11 – Схема квадратора (а) и условное обозначение (б)

     Если соединить входы х₁ , у₁  с выходом и заземлить входы x₂,y₂,z₂, то получим схему извлечения квадратного корня

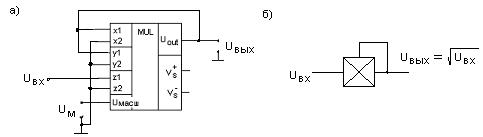
Рисунок 4.12 – Схема извлечения квадратного корня (а) и

условное обозначение (б)

 

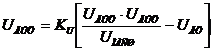
При К_U>>1                                      U_вых/K_U →0,       тогда

 или .

 

 

4.3 Нелинейный режим работы ОУ

 

     Если U_вх < │U_гр│, то ОУ работает в линейном режиме. При  U_вх > │U_гр│ ОУ работает в нелинейном ключевом или импульсном режиме (рис.4.13,а).

 

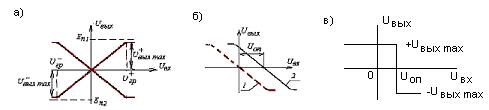
Рисунок 4.13 – Амплитудные характеристики ОУ без смещения (а) и со смещением (б)

     При подаче на один из входов ОУ постоянного напряжения амплитудная характеристика по другому входу смещается на это же значение. Например, на неинвертирующий вход  ОУ (рис.4.13,б) подано напряжение +U_оп, тогда характеристика по инвертирующему входу (кривая 1) сместится на значение U_оп вправо (кривая 2). На (рис.4.13,в) приведена амплитудная характеристика инвертирующего ОУ с опорным напряжением на неинвертирующем входе в ключевом режиме работы – амплитудная характеристика компаратора.

 

4.3.1 Аналоговый компаратор

 

     Аналоговый компаратор (рис.4.14,а) применяется для сравнения аналогового сигнала с опорным напряжением. На (рис.4.14,а) на неинвертирующий вход подано  опорное напряжение U_оп, на инвертирующий вход напряжение U_вх.

     При этом выполняются условия (рис.4.14,б):

если: U_вх< U_оп, то   U_вых = U⁺_выхmax,

если U_вх > U_оп, то   U_вых = U^-_выхmax.

     При равенстве U_вх = U_оп,  U_вых = 0. Так как коэффициент усиления ОУ равен сотни тысяч, то компаратор переключается на противоположное значение.

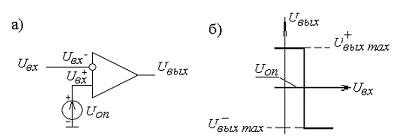
Рисунок 4.14 – Схема компаратора на ОУ

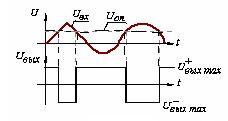
Рисунок 4.15 – Временная диаграмма работы компаратора

    

4.3.2 Триггер Шмидта

 

     Релаксационными называют генераторы, у которых усилитель работает в переключающем (релейном) режиме. К ним относят автоколебательный и ждущий мультивибраторы, генераторы пилообразных и треугольных колебаний. Основой релаксационных генераторов на ОУ является обычно регенеративный компаратор, называемый триггером Шмитта (ТШ). Регенеративный компаратор может быть выполнен на ОУ с резистивной ПОС.

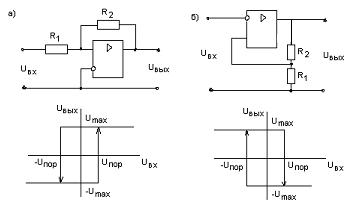
Рисунок 4.16 – Триггер Шмитта: а – неинвертирующий; б – инвертирующий

     Переходная характеристика компаратора имеет гистерезис, ширина которого равна удвоенному пороговому напряжению 2U_пор, при чем для схемы неинвертирующего (рис.4.16,а)

а для инвертирующего компаратора (рис.4.16,б)

где U_max – максимальное выходное напряжение ОУ (насыщение) в зависимости от типа ОУ.

     Триггер Шмидта имеет два состояния устойчивого равновесия и преобразует аналоговый сигнал в импульсный. Если подать напряжение на вход, связанный с землей в любой схеме (рис.4.16), то амплитудная характеристика ОУ сместится вправо или влево в зависимости от полярности приложенного напряжения. Для примера рассмотрим схему инвертирующего ТШ с опорным напряжением +U_оп (рис.4.17,а).

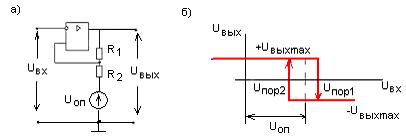
Рисунок 4.17 – Схема инвертирующего ТШ с опорным напряжением (а) и его амплитудная характеристика (б)

     Резисторы R₁ и  R₂ создают ПОС, которая обеспечивает лавинообразное  переключение выхода триггера из положительного в отрицательное и наоборот. Пороговые напряжения (рис.4.17,б), при которых происходит переключение триггера, определяются как

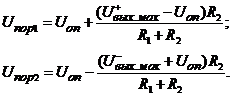
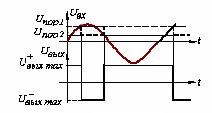
Рисунок 4.18 – Временная диаграмма работы ТШ

     Из (рис.4.18) видно, что при U_вх = 0, на выходе U_вых = U⁺_выхmax, так как на неинвертирующем входе U_вх +Uоп>0. Когда  U_вх возрастет до U_пор1, равное смещению Uвх+ триггер переключается в U_вых = U^-_выхmax. За счет положительной обратной связи R₁,R₂  смещение на U_вх+ мгновенно станет равным U_пор2. Когда U_вх уменьшится до U_пор2, произойдет обратное переключение триггера в U_вых = U⁺_выхmax и т.д. Так как пороговое напряжение U_пор меняется от одного значения U_пор1 к другому U_пор2.